Water waves propagating over mud often lose energy, resulting in a decrease of wave height and possibly refraction and diffraction of the waves. The bottom of the Gulf of Mexico offshore of Louisiana has large areas of mud as do many other areas in the world.
Water waves interact with muddy bottoms in a variety of ways listed below. We will refer to these interactions by letter:
A. Direct wave interactions: the fluid mud motion is directly forced by the particle orbital velocity and pressure gradient of the surface waves.
B. Indirect wave interactions: the fluid mud motion is forced by nonlinear effects of the surface wave-wave interactions.
C. Resonant wave-wave interactions: (strong) resonant nonlinear interactions between surface waves and water-mud interfacial waves. These generally occur over greater spatial-temporal scales with unique propagation characteristics.
D. Shear instability and turbulent mud-flow interactions: Surface waves induce a shear flow instability at the lutocline, which has been observed in the field (Traykovski et al., 2000).
E. Large-scale broadband mechanisms: the presence of broadband surface waves and multi-scale interactions over varying wave/bottom conditions involving or combining the above mechanisms leads to features not predicted in the context of a single wave or wave combination or interaction mechanism.
The major objective of this study is to examine the various mechanisms of water wave dissipation over muds. We will use three approaches:
- Field measurements off the coast of western Louisiana to examine in detail the behavior of a mud bottom during wave events, providing the means to determine the operative damping mechanisms there
- Secondly, we will carry out laboratory experiments of waves over mud in two large wave tanks to isolate the mechanisms in greater detail: one tank is at the Johns Hopkins University and the other is the Super Tank at the Tainan Hydraulics Laboratory, Taiwan.
- Finally, theoretical analysis and numerical modeling will provide the input for determining dissipation algorithms to be added into a phase-resolved computational model based on high order spectral methods (SNOW, developed at MIT) and spectral forecast models, such as SWAN.
The Participants
Johns Hopkins University

 Robert A. Dalrymple, Principal Investigator and Laboratory Team Leader
Robert A. Dalrymple, Principal Investigator and Laboratory Team Leader

 Lian Shen
Lian Shen
Massachusetts Institute of Technology

 Yuming Liu
Yuming Liu

 Chiang C. Mei
Chiang C. Mei

 Dick K.P. Yue, Theory Team Leader
Dick K.P. Yue, Theory Team Leader
Woods Hole Oceanographic Institution

 Peter Traykovski
Peter Traykovski

 John Trowbridge, Field Team Leader
John Trowbridge, Field Team Leader
Boston College

 Gail C. Kineke
Gail C. Kineke
Louisiana State University

 Samuel J. Bentley
Samuel J. Bentley
National Cheng Kung University

 Hwung-Hweng Hwung, Cooperating Laboratory Director, Tainan Hydraulics Laboratory
Hwung-Hweng Hwung, Cooperating Laboratory Director, Tainan Hydraulics Laboratory
The Field Program
The objectives of the field measurement program are to quantify the characteristics and dynamics of the seabed and the dissipative wave bottom boundary layer and to determine the terms in a simplified wave energy budget:
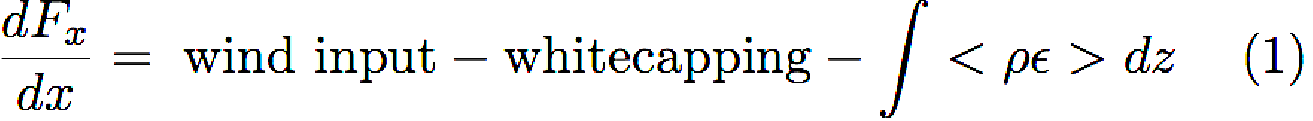 where x and z are cross-isobath and vertical coordinates, Fx is the cross-isobath component of the wave energy flux, ρ is the density of the fluid-sediment mixture, ε is the dissipation rate per unit mass, the vertical integral is over the thickness of the bottom boundary layer, and brackets denote an average over many wave periods. The measurements and analysis will focus on determining whether the dissipative wave bottom boundary layer is due to (i) an essentially laminar flow of a sediment-laden layer with enhanced viscous or elastic properties influenced by gravity waves that are coherent with the surface waves, as has been assumed in numerous theoretical studies and realized in laboratory experiments (Gade 1958; Dalrymple and Liu, 1978; MacPherson, 1980; Jiang and Zhao, 1989; Ng, 2000), or (ii) a turbulent flow of a sediment-stratified fluid with no wave-like motions other than small-scale Kelvin-Helmholtz instabilities, as has been observed in previous field studies (Trowbridge and Kineke, 1995; Traykovski et al., 2000). Our hypothesis is that (i) and (ii) are end-members of a continuum of states that are realized by oceanic sediment-laden wave-driven flows, depending on the forcing and seabed conditions. The proposed field measurement program will combine, for the first time, quantitative measurements of wave evolution due to shoaling and dissipation with modern acoustical measurements of seabed processes at a muddy site on a continental shelf exposed to surface waves.
where x and z are cross-isobath and vertical coordinates, Fx is the cross-isobath component of the wave energy flux, ρ is the density of the fluid-sediment mixture, ε is the dissipation rate per unit mass, the vertical integral is over the thickness of the bottom boundary layer, and brackets denote an average over many wave periods. The measurements and analysis will focus on determining whether the dissipative wave bottom boundary layer is due to (i) an essentially laminar flow of a sediment-laden layer with enhanced viscous or elastic properties influenced by gravity waves that are coherent with the surface waves, as has been assumed in numerous theoretical studies and realized in laboratory experiments (Gade 1958; Dalrymple and Liu, 1978; MacPherson, 1980; Jiang and Zhao, 1989; Ng, 2000), or (ii) a turbulent flow of a sediment-stratified fluid with no wave-like motions other than small-scale Kelvin-Helmholtz instabilities, as has been observed in previous field studies (Trowbridge and Kineke, 1995; Traykovski et al., 2000). Our hypothesis is that (i) and (ii) are end-members of a continuum of states that are realized by oceanic sediment-laden wave-driven flows, depending on the forcing and seabed conditions. The proposed field measurement program will combine, for the first time, quantitative measurements of wave evolution due to shoaling and dissipation with modern acoustical measurements of seabed processes at a muddy site on a continental shelf exposed to surface waves.
Our observations will include shipboard sampling and in-situ time-series measurements. The design of the time-series observations is based on an approach in which measurements of waves are obtained at the seaward and landward edges of a control volume to determine the divergence of wave energy flux on the left side of equation (1); atmospheric measurements are obtained within the control volume to permit the estimation of the wind input and whitecapping terms in (1); and detailed measurements of near-bottom processes are obtained within the control volume to determine the near-bottom energy sink in (1) and to characterize and quantify the near-bottom dissipative processes. The bottom dissipation measurement array is designed to sample both long wavelength mud waves [(i) above] and turbulent instabilities on the mud-water interface [(ii) above] as measurements that only account for the long wavelength processes will alias the shorter scales. The purposes of the shipboard sampling are to obtain detailed information about the structure of the seabed from cores and to characterize the spatial variability of water-column processes and seabed characteristics in the region of the control volume, which will aid in the precise site selection as well as in data interpretation.
Our measurement site is on the inner shelf offshore of the Atchafalaya River (Figure 1), where dense muds have been observed annually during and after high discharges from the Atchafalaya and Mississippi Rivers, between approximately February and May (Rotondo and Bentley, 2003, 2004; Draut et al., 2005a, 2005b), and where intense dissipation of wave energy caused by seabed processes has been observed (Figure 2; see also Sheremet and Stone, 2003; Sheremet et al., 2004; Higgins, 2002). The time-series measurement sites will be near existing oil platforms to provide protection from fishing activities, a strategy successfully used by Kineke to obtain the measurements described in the Higgins (2002) thesis (Figures 1 and 2). The offshore, central and onshore sites for the control volume occupied by the time-series instrumentation will be at water depths of approximately 15, 10 and 5 m (Figure 1). The instrument deployments and recoveries and the shipboard measurements will be carried out with the Louisiana Universities Marine Consortium (LUMCON) Research Vessel Acadiana.
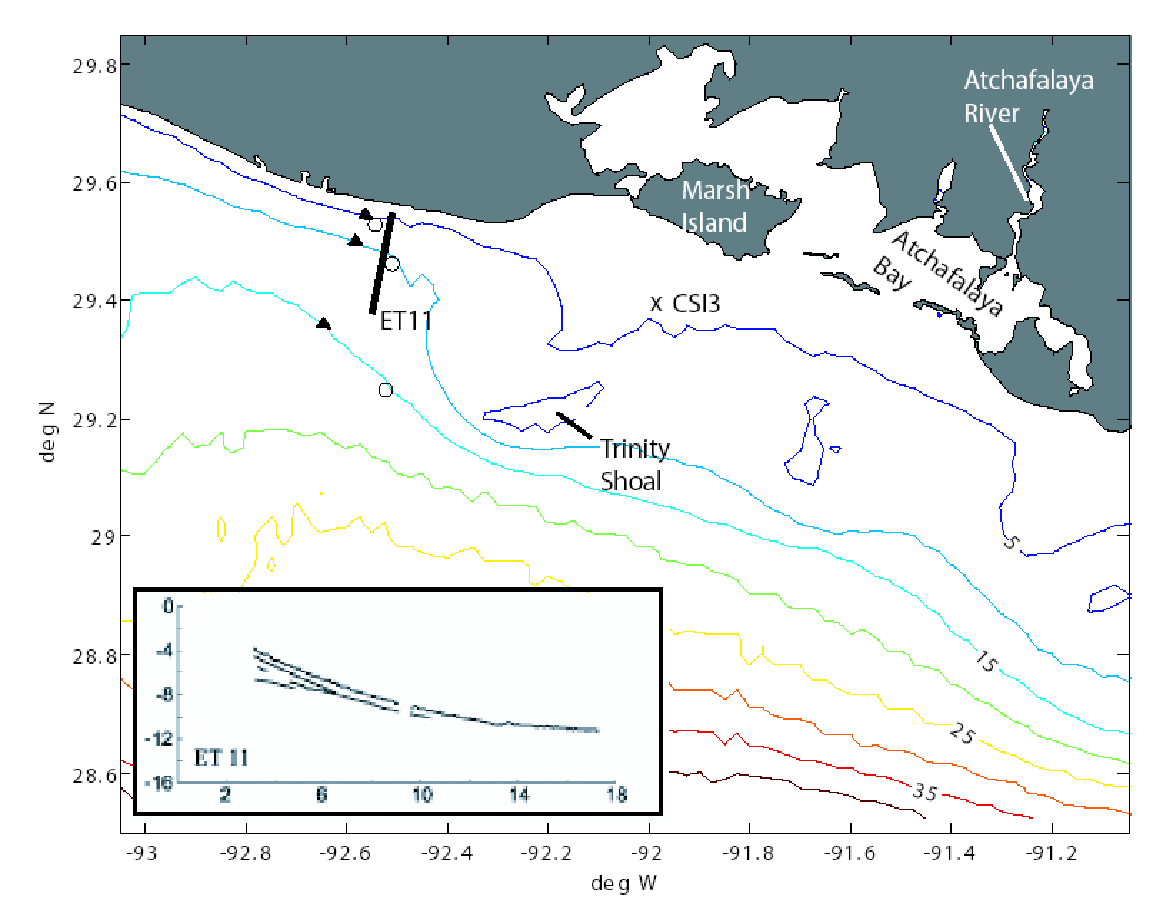 Figure 1. Site map of the Louisiana coast, showing locations of the 1999 wave measurements reported by Higgins (2002) (o), the location of a dual-frequency echosounder transect (solid line), the results of the echosounder transect (inset), Louisiana State University’s measurement station CSI3, and the locations of the wave and bottom boundary layer measurements proposed here (s). The echosounder results show an unconsolidated high-porosity mud layer with a thickness of approximately 1 m overlying consolidated mud and extending seaward from a water depth of 4 m.
Figure 1. Site map of the Louisiana coast, showing locations of the 1999 wave measurements reported by Higgins (2002) (o), the location of a dual-frequency echosounder transect (solid line), the results of the echosounder transect (inset), Louisiana State University’s measurement station CSI3, and the locations of the wave and bottom boundary layer measurements proposed here (s). The echosounder results show an unconsolidated high-porosity mud layer with a thickness of approximately 1 m overlying consolidated mud and extending seaward from a water depth of 4 m.
The field measurement schedule will be as follows. A pilot experiment will occur in February and March of 2007, and a main experiment will occur during February and March of 2008. The pilot experiment will identify the depths where fluid mud is found during energetic wave events, and the precise location of the main experiment will be chosen to sample these processes optimally. An experiment at a new site, chosen to quantify the effect of a different water depth or bottom type (e.g., ratio of mud to sand), will occur during February and March of 2010. Each measurement period will have a duration of two months, split into two one-month deployments separated by a brief instrument turnaround for offloading data, cleaning sensors and replacing batteries. Shipboard sampling for periods of approximately four days will be conducted during every instrument deployment, turnaround, and recovery.
The atmospheric measurements at the central time-series site (Figure 1) will be obtained from a surface buoy instrumented with an RM Young anemometer, which measures wind speed and direction; a Vaisala PTU2000 sensor, which measures atmospheric relative humidity, temperature, and pressure; and a Seabird temperature sensor, which will measure the near-surface oceanic temperature. Time-series measurements of waves at the landward and seaward ends of the control volume will be obtained by RDI 1200 kHz acoustic Doppler current profilers (ADCP) with waves enhancement, which will be mounted on trawl-resistant bottom tripods. The ADCP measurements will provide estimates of the directional wave spectrum and the frequency-direction distribution of the wave energy flux. The landward and seaward tripods will have downward aimed acoustic backscatter profilers to determine thicknesses and concentrations of fluid mud layers at these sites.
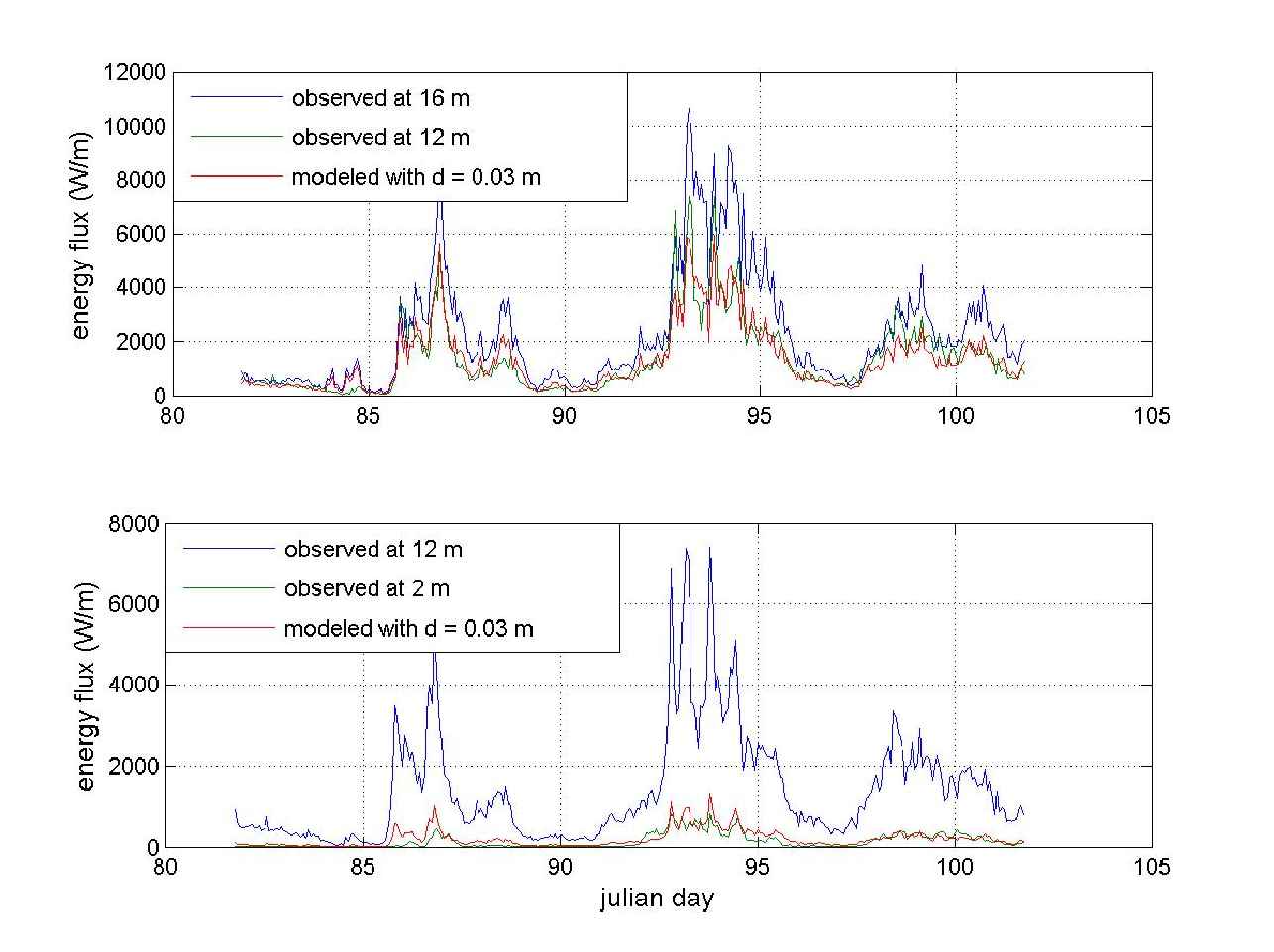 Figure 2. Onshore wave energy flux determined from measurements reported by Higgins (2002) and model calculations based on linear frictional shoaling theory (e.g. Dean and Dalrymple, 1991) with a two-layer viscous fluid model of the muddy seafloor (Dalrymple and Liu, 1978). The constant thickness d and viscosity of the mud layer in the model computations have been selected to optimize the agreement with observations. Calculations based on a quadratic drag law with optimized constant and large (0.1) wave friction factor fw reproduce the measurements with equal success, as do calculations based on a visco-elastic model (MacPherson,1980) with optimized constant viscosity. Winds were persistently northward (toward shore), so that wave damping by adverse winds did not occur. Estimates of wind forcing and whitecapping based on simple models (Janssen, 2004) indicate that these processes had a non-negligible but minor effect.
Figure 2. Onshore wave energy flux determined from measurements reported by Higgins (2002) and model calculations based on linear frictional shoaling theory (e.g. Dean and Dalrymple, 1991) with a two-layer viscous fluid model of the muddy seafloor (Dalrymple and Liu, 1978). The constant thickness d and viscosity of the mud layer in the model computations have been selected to optimize the agreement with observations. Calculations based on a quadratic drag law with optimized constant and large (0.1) wave friction factor fw reproduce the measurements with equal success, as do calculations based on a visco-elastic model (MacPherson,1980) with optimized constant viscosity. Winds were persistently northward (toward shore), so that wave damping by adverse winds did not occur. Estimates of wind forcing and whitecapping based on simple models (Janssen, 2004) indicate that these processes had a non-negligible but minor effect.
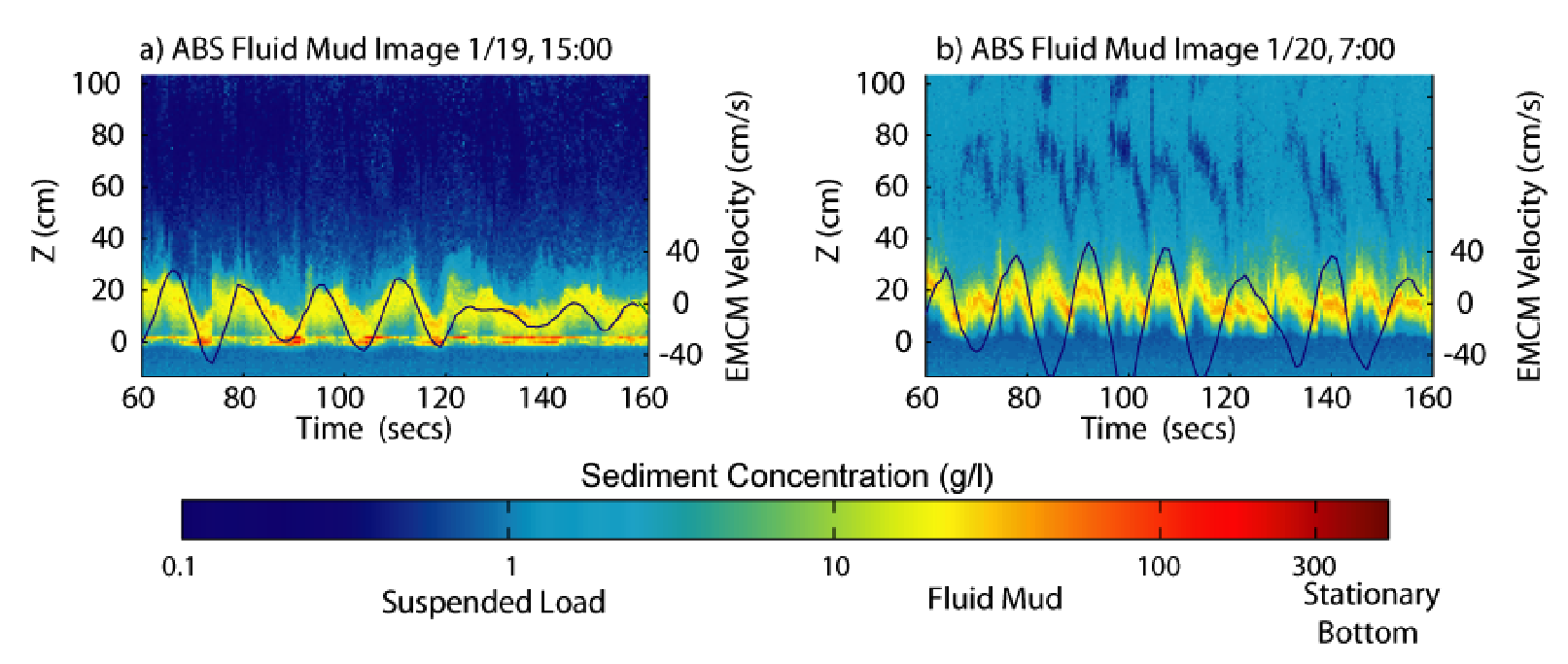 Figure 3. Waves on the lutocline (mud-water interface) as imaged by a 2.5 MHz acoustic backscatter sensor (ABS) during the Eel River Strataform program in 60 m water depth (Traykovski et al., 2000). Surface gravity wave velocities at 50 and 100 cm above bottom are shown as solid lines. The thick yellow region shows the lutocline. Wave spectra (not shown) indicate a single peak at a frequency of approximately 0.07 Hz. Spectra of lutocline elevation (not shown) show peaks at the wave frequency and harmonics at 2 and 3 times the wave frequency.
Figure 3. Waves on the lutocline (mud-water interface) as imaged by a 2.5 MHz acoustic backscatter sensor (ABS) during the Eel River Strataform program in 60 m water depth (Traykovski et al., 2000). Surface gravity wave velocities at 50 and 100 cm above bottom are shown as solid lines. The thick yellow region shows the lutocline. Wave spectra (not shown) indicate a single peak at a frequency of approximately 0.07 Hz. Spectra of lutocline elevation (not shown) show peaks at the wave frequency and harmonics at 2 and 3 times the wave frequency.
The design of the acoustical time-series measurements of near-bottom processes within the control volume (Figure 1) is based on extensive experience with measurements over muddy seafloors on the Eel River shelf during the ONR-funded STRATAFORM program (Traykovski, 2000), during which a pronounced lutocline characterized by wave-like disturbances was clearly observed (Figure 3). The near-bottom measurements will be obtained from a quadrapod (Figure 4) instrumented with a horizontal array of vertically oriented pulse-coherent pencil-beam Doppler sonars. These sonars, which are similar to the Sontek "Dopbeam," are a new technology being developed at WHOI, which will provide improved measurements of echo intensity, low power requirements for battery-powered deployments, and lower cost than the Dopbeams. The array of vertically oriented Doppler sonars will measure the vertical structure of echo intensity and vertical velocity at multiple horizontal positions along vertical paths with ranges of approximately 1 m and resolution of approximately 0.01 m. The vertical sonars at each end of this array will be complemented by an obliquely oriented fanbeam Doppler receiver, which will produce a vertical profile of horizontal velocity measurements. The temporal sampling and horizontal spacing of the sonar array (Figure 4) is designed to resolve both the anticipated wavelengths of the interfacial instabilities (0.5 to 3 m based on a linear stability analysis), and the smaller-amplitude mud waves, which are hypothesized to have the same length as the surface gravity waves (20 to 50 m). A rotating pencil-beam sonar will be used to measure the horizontal and temporal variability of lutocline elevation on horizontal scales of meters with spatial resolution of centimeters. Time-series measurements of surface waves and wave-induced near-bottom velocities will be made at the quadrapod with an ADCP and acoustic Doppler velocimeters (Figure 4).
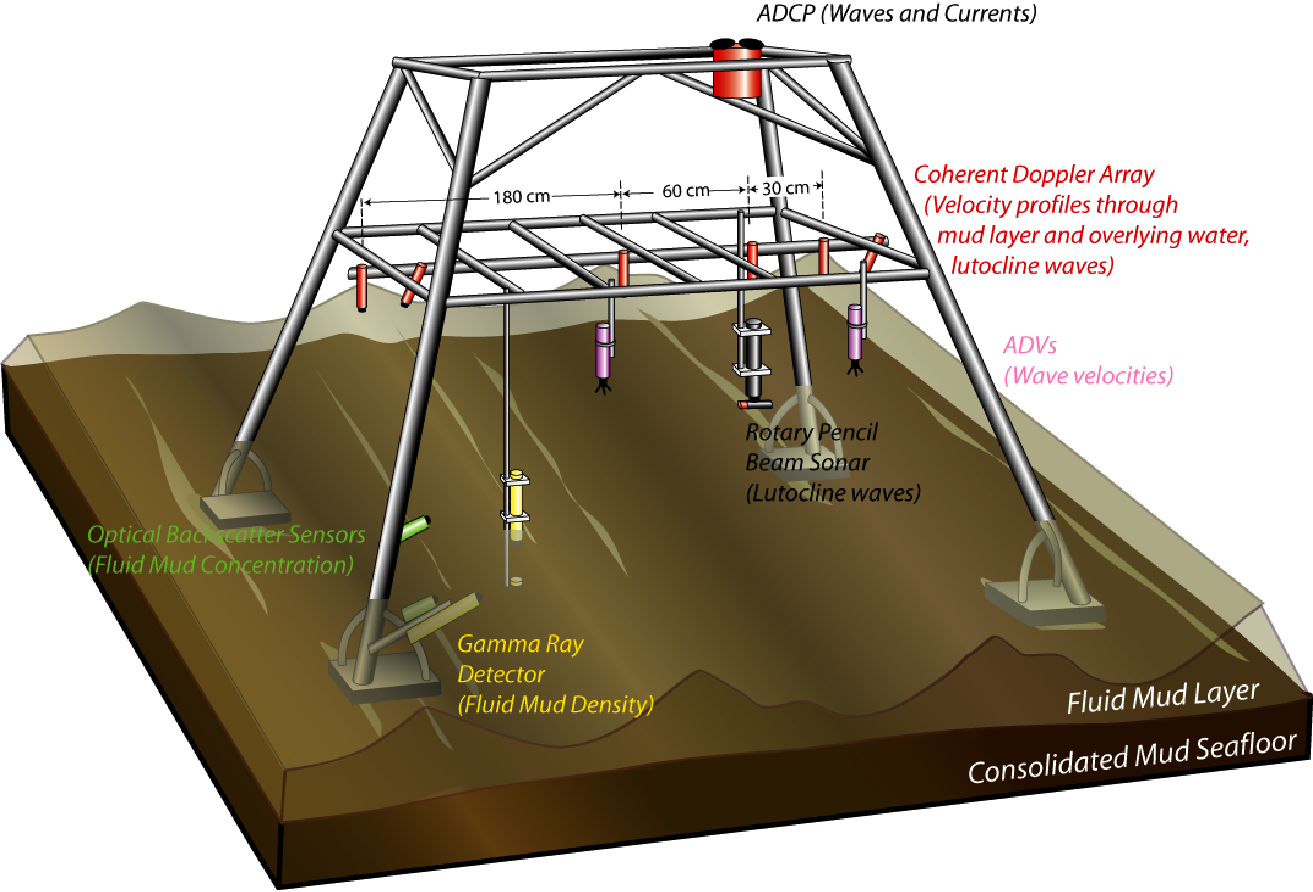 Figure 4. The suite of instrumentation to measure boundary layer processes associated with the dissipation of waves by a muddy seafloor. A coherent Doppler array will measure both mud-water interface turbulent instabilities and long wavelength mud-waves that are coherent with surface gravity waves. A gamma ray source-detector instrument and optical backscatter instruments will provide additional measurements of sediment concentration within the fluid mud layer. An ADCP and ADVs will measure the local forcing hydrodynamics for the near-bed sediment processes.
Figure 4. The suite of instrumentation to measure boundary layer processes associated with the dissipation of waves by a muddy seafloor. A coherent Doppler array will measure both mud-water interface turbulent instabilities and long wavelength mud-waves that are coherent with surface gravity waves. A gamma ray source-detector instrument and optical backscatter instruments will provide additional measurements of sediment concentration within the fluid mud layer. An ADCP and ADVs will measure the local forcing hydrodynamics for the near-bed sediment processes.
Shipboard measurements during deployment, turnaround and recovery cruises will include high-resolution acoustic sub-bottom profiles with an Edgetech Chirp 424 towfish, which will image the horizontal and vertical structure of the fluid mud layers (Figure 1); water-column measurements with a profiling tripod (Sternberg et al., 1991), which will characterize properties of fluid muds and provide ground truth for calibration of acoustic and optical measurements; and boxcores, which will provide detailed information about the seafloor (Figure 5). Analysis of boxcores will include profiles with a gamma densitometer (developed by Bentley using a Cs-137 source and a Canberra NaI gamma detector), which will provide 1-cm resolution density measurements of the transition zone between the lutocline and the consolidated seabed; sediment grain size distribution (with a Micromeritics Sedigraph 5100); 210Pb, 7Be, and 137Cs radioisotopes (using Canberra LeGe gamma-decay detectors), which will document and quantify sediment flux, reworking, and deposition (Sommerfield et al. 1999; Rotondo & Bentley 2003, 2004); and X-radiography, which will determine sedimentary bedding and structures. Analysis of boxcore samples will also include measurements of viscosity using a Couette viscometer with time-dependent forcing (Isobe et al., 1992) and acoustical shear wave propagation speeds.
The analysis of the field measurements will focus on estimation of the terms in (1) and characterization and quantification of the near-bottom dissipative processes. Estimates of directional wave spectra will be obtained from the ADCP measurements by using standard RDI software, and estimates of the frequency distribution of the wave energy flux will be obtained from the wave spectra. The proposed atmospheric and near-surface measurements are sufficient to provide estimates of atmospheric fluxes of momentum and buoyancy based on bulk formulae (e.g. Fairall et al., 2003) and to provide estimates of energy fluxes to waves due to wind input and whitecapping, respectively, based on empirical and semi-empirical formulae (e.g. Janssen, 2004). The combination of acoustical and gamma-ray measurements will determine the thickness and concentration of the near-bottom sediment-laden layer. The horizontal array of coherent Doppler sonars will determine the horizontal and vertical structure of the sediment concentration and will permit identification and quantification of interfacial waves and Kelvin-Helmholtz instabilities. Horizontal velocities and sediment concentrations determined from the vertically and obliquely oriented sonar array will determine the vertical structure of the velocity within the sediment-laden bottom boundary layer and will permit inferences of shear stresses (based on the standard first-order horizontal momentum equation for the bottom boundary layer), dissipation rates (the product of shear stress and rate of shear strain), and effective viscosity (the ratio of shear stress to rate of shear strain). Velocities measured by the sonars will provide inertial-range estimates of the dissipation rate of turbulent kinetic energy. Inferences of mechanical seafloor properties obtained from analysis of boxcores will permit quantitative evaluation of viscous and viscoelastic model computations. The analysis will be complemented by simulations of regional wave propagation based on the Simulating Waves Nearshore (SWAN) model, which will be implemented for the study site as part of the proposed project. The field results will be synthesized with results based on laboratory experiments and analytical and numerical models.
The Laboratory Program
Two wave tanks and one wave basin will be used in the laboratory studies. One tank is at Johns Hopkins University in the Coastal Engineering Laboratory. The second wave tank is the Super Tank of the Tainan Hydraulic Laboratory (THL) of the National Cheng Kung University, Taiwan, under the direction of Dr. H.-H. Hwung, who is cooperating with this project. The THL also has a wave basin that they will fill with mud to examine diffractive effects of mud.
The wave tank at Johns Hopkins University will be used to carry out a series of experiment concerning wave damping over muds, with the view of examining the details of the mechanisms of damping. The wave tank is rather wide: 2.5 m, with a length of 18.3 m and a depth of 1.7 m. It has four hydraulically-actuated piston wave paddles at one end. The paddles are individually computer-controlled, permitting the creation of directional sea states in the wave tank. A wave absorbing section will be added to the other end of the tank to remove waves with small reflection back into the test section. The tank has large glass panels at two locations along the tank. The bottom of the wave tank will be modified by adding a 10 m long section into which about 10 cm mud will be placed. False floor sections will be emplaced before and after the mud section as depth transitions.
We will use commercially available kaolinite muds, which have been used in laboratories for wave damping experiments previously (e.g., Isobe et al., 1992; Soltanpour et al., 2004). The mud characteristics will be varied by using different water contents. We will use two different muds: a very fluid mud, which behaves as a viscous liquid, and a more dense mud, which will not respond as readily to the wave forcing. In addition, a mud similar to that observed in the field will be tested. The scaling of the field situation will be done based on the type of mud response that occurs. For fluid muds, the dimensionless parameters between the field and the laboratory, from Dalrymple and Liu (1978), are the relative mud depth, d/h, where h is the water depth and d is the mud layer thickness, and the ratio of the fluid mud upper boundary layer thickness to the mud layer thickness: d (σ/2ν)0.5 , where ν is the mud viscosity. To model the waves, the Froude number should be the same as in model and prototype.
The rheology of the laboratory clay will be tested with a rotary shear meter as designed and used by Isobe et al. (1992). The advantage of the rotary shear meter is that it is a programmable Couette viscometer, allowing the testing of the mud with a variety of time-dependent and oscillatory shear rates. This same instrument (built for this project) will be used in the field as well, so that the laboratory muds can replicate, as closely as possible, the field conditions. The rotary shear meter consists of a movable inner cylinder placed within a larger fixed outer cylinder, with the mud placed between the two cylinders. The inner cylinder then is rotated with oscillatory motions, or a combination of oscillatory and mean motions, simulating wave and current effects on the mud. Isobe et al. (1992) showed that there is a considerable hysteresis in the stress/strain rate for oscillatory forcing.
The first test series will examine direct wave damping (Type A) and the sediment response to monochromatic incident wave trains. Eight wireless capacitance wave gages will be located down the centerline of the tank (one prior to the test section and one after--the remaining six within the section). These gages will be used to determine the wave height decay with distance. A digital video camera, shooting through the glass side wall, will permit the observation of the mud response in all the tests. However, Tsuruya and Nakano indicate that the mud wave height may vary across the width of the tank. Therefore, two additional capacitance gages will submerged and placed in the mud to determine the mud wave variation between the middle and the glass sidewall. Since these gages will be synchronized to the surface wave gages, the phase shift between the surface water waves and the mud waves will be determined. To determine the fluid velocities above the mud waves, a Nortek Vectrino 3D ADV will be used. During two of the tests (periods 2 and 5), the line array of Doppler sonars from the field quadrapod will be brought into the wave tank for a series of tests similar to the field situation. These tests will help to determine what is observed in both the laboratory and the field. Dyed mud (Sakakiyama and Bijker, 1989) will be placed into vertical profiles and sampled for mud mass transport, which occurs, like Stokes drift, because of the nonlinearities in the wave-induced motions of the sediment.
To obtain significant wave-mud interaction, a reasonable amount of wave damping has to occur within the mud test section, which means the test section has to be several wavelengths long. In order that the field acoustical equipment fit within the wave tank, some of our tests will be carried out in a minimum of 0.6 m of water. We will be testing waves from 0.9 s period (7 waves in our test section) to about 2 s period (2.4 waves in test section); this leads to kh values of 3 to 0.8, ranging from deep to nearly shallow water waves. (Sakakiyama and Bijker had about 9 waves in their test section.) Shallower water depths will be used if more wave lengths are needed in the test section. We will also be varying the wave height to examine nonlinear effects on damping rates.
Analyses of these laboratory experiments will provide information about the mud behavior and the type of mechanism that applies to the type of mud used. Based on the experience of others, we will likely find that the damping rate of waves over the mud will depend on the frequency of the incident wave train as will the amplitude of the bottom response. Sakakiyama and Bijker (1989) show that bottom responses of up to 20 percent of the surface wave amplitude can occur. We also expect that a maximum energy loss will occur as a function of wave frequency.
As part of this series of monochromatic tests, we will be examining whether there is evidence of nonlinear mechanisms for wave damping in the laboratory (Type C). Foda (1989) indicates that the sidebands created by the Benjamin-Feir instability of surface waves are more rapidly damped by a soft bed; this may not be observable in our short tank. Hill and Foda (1998) examine the case where a single surface wave train can create, through nonlinear interactions, two interfacial mud waves.
The second series of tests are to model the field situation and to use the field Doppler array in the laboratory. The waves will be driven with field observed spectra. The mud will have a viscosity similar to that found in the field. The advantage of the laboratory in this case is that we can see the bottom that the sonar system is detecting (not so in the field). We will be comparing the measurements made by lab instrumentation with that of the sonar.
A third set of experiments will be carried out examining the nonlinear damping of wave groups (Type B). The first runs will be with two collinear wave trains with very similar frequencies, which will create wave groups and their associated bound long wave. The wave trains will have periods chosen such that they are deep water waves not affected by the presence of a mud bottom. However the bound wave will be a longer wave that interacts with the bottom. It is the hypothesis of Sheremet and Stone (2003) that the bound long wave leads to the damping of deep water waves over muds. We will chose the frequency of the bound long wave such that it corresponds to a wave period that is optimally damped over the mud, thus maximizing the likelihood of observing this mechanism in the laboratory. A major observation of this test will be the damping rates of the short waves as a measure of the energy transfer into the bound long wave and then into the soil. A companion experiment will be carried out in the super tank at the THL to examine a different scenario and a different scale.
The fourth series of tests will involve directionality of the incident wave trains. The wide wave tank permits the creation of intersecting wave trains of given angle that propagate down the tank. We will be examining the occurrence of Hill and Foda's mechanism and other nonlinear mechanisms (Type C). The directionality of waves will be examined also in the nearshore basin at the THL. However, the purpose of those tests will be the diffractive effects of a mud patch on the wave directionality.
A series of experiments will be developed to examine the behavior of the lutocline. We hope to observe optically the occurrence of shear instability of the boundary layer (Type D). Measurements will examine the damping and the motion of the underlying mud. Finally, spectral runs will be made (Type E) to look at the damping mechanisms for a wide banded spectrum. During these tests, the field Doppler array will again be brought into the lab to make measurements.
Based on the laboratory experiments, we will obtain a measure of how effective each of the various mechanisms are in damping. This will help shape the theory and numerical modeling effort as they will be focusing on the most likely and the most effective damping mechanisms.
The Theoretical Program
We propose integrated comprehensive theoretical analysis and numerical modeling, closely coupled with the proposed field measurements and laboratory tests, to investigate each of the mechanisms we identify. The immediate objective is theoretical framework and understanding and canonical results; the intermediate objective is parameterization and modeling at multi-scales; the final objective is effective large-scale direct (phase-resolved) simulations and extensions of spectral wave prediction models, such as SWAN, for wave propagation over muddy seabeds.
A. Direct wave interactions: Damping mechanisms for fluid muds governed by a Newtonian shear stress are well-known (e.g., Dalrymple and Liu, 1978) and are readily input into existing numerical models. We will investigate the direct interaction mechanisms theoretically in the context of inviscid water waves over a laminar flow Bingham mud layer, and Poincaré perturbation, (Mei, 1989; Mei, Stiassnie, and Yue, 2005, p.472ff).
The theoretical results above lead naturally to modeling by phased-resolved large-scale simulations (SNOW), and, in particular, suggest the form of the modifications of the bottom dynamic and kinematic boundary conditions to capture the dissipative and dispersive effects of the mud-layer dynamics. Simulations will be obtained for select field and laboratory conditions to obtain the necessary quantitative cross-calibration and parameterization.
B. Indirect wave interactions: We consider the general nonlinear problem of surface wave-wave interactions and their direct coupling with the mud flow. The mechanism of damping of set-down long waves by muddy seabed hypothesized by Sheremet et al. (2004) is a special case.
For modeling, indirect wave interactions can be incorporated in a manner similar to direct interactions. The key extension is the inclusion of higher-order nonlinear interactions in SNOW. To account for feedback to the short wave evolution, it is necessary to include wave-wave interactions at least to third order.
C. Resonant wave-wave interactions: Strong resonant interactions of surface waves and interfacial waves offer a possibly effective mechanism to transfer surface wave energy to interfacial mud layer waves. The resonant exchange among the (surface-mud) waves satisfies specific conditions on the wavelengths, frequencies and directions of these components as a function of the mud layer properties and might therefore be especially relevant in the context of remote detection and determination of seabed characteristics. Our theoretical treatment assumes discrete layers with constant properties and accounts for the coupled nonlinear dynamics of surface and internal waves in these layers. Initially, two layers are considered corresponding to respectively clear water (inviscid irrotational) and fluid mud (non-Newtonian). The multiple-scale analysis is an extension of irrotational waves for this problem where triad resonances obtain at second order (e.g. Hill and Foda, 1998; Jamali et al., 2003). The dissipation effect of the mud layer may now be considered, for example, using equivalent (Newtonian) viscosity. In the more general case, the analysis may be generalized to multiple (mud) layers involving different properties (such as concentration).
The resonant interactions above can be modeled in an extension of SNOW to the case involving (multiple) internal layers. For inviscid irrotational flow in stratified water, this extension has recently been obtained (Alam, Liu and Yue, 2005) in two- and three-dimensions to arbitrary high order. The inclusion of viscous dispersion and dissipation effects within the submarine layers requires special modeling of interfacial boundary terms which might be linear (with constant or variable coefficients) or nonlinear. The key to the modeling effort is the availability of field data for relatively long distances (or time) under conditions (e.g. relatively thick mud layer depth with low mud concentration) where strong surface-mud resonant interaction obtains.
D. Shear unstable and turbulent mud-flow interactions: We analyze theoretically the shear flow instability at the water-mud interface assuming a Bingham mud fluid modeled by power law. Linearized instability is analyzed first taking into account the non-Newtonian behavior of fluid mud subject to appropriate bottom and mud-water interface boundary conditions, and the resulting Orr-Sommerfeld eigenvalue problem is solved numerically (Shen, Triantafyllou and Yue, 2000; Shen, Zhang and Yue, 2002).
The shear flow instability and subsequent potential development into turbulent flow will also be investigated for small scale (order of water wavelength) and relatively low effective Reynolds numbers (O(103)) using direct numerical simulations (DNS). These DNS are built on existing capabilities developed for turbulent flow-moving bottom problems (Shen et al., 1999; Shen et al., 2003). For larger scale and higher Reynolds numbers for fully developed turbulent mud flow, a large-eddy simulation (LES) approach is adapted, in which sub-grid scale (SGS) terms are modeled based on theoretical results and DNS (cf. Shen and Yue, 2001). The key development in both DNS and LES is the numerical treatment of visco-plasticity. In this study we employ a viscosity regularization or smoothing method (Glowinski, 1983; Frigaard and Nouar, 2005). Guided by tank and field data, different regularizing functions (Bercovier and Engleman, 1980; Pananastasiou, 1987; Allouche, Frigaard, and Sona, 2000) are systematically tested and evaluated.
Wave interactions with underlying turbulent mud flow can be modeled in SNOW in the framework of two interacting fluid layers. The irrotational surface wave motion is coupled, across a matching/patching boundary, to an underlying turbulent mud-layer. For large scales, the latter is described using large-wave simulation (LWS), in which the full equations are filtered at sub-surface-wavelength scales. The resulting sub-wavemode-scale stresses require special closure modeling based on laboratory and field measurements with guidance from DNS and LES.
E. Large-scale broadband mechanisms: The general problem of practical interest involves broadband waves propagating over complex/varying muddy seabeds of length O(10) km or more. The field measurement proposed is indeed a problem of this nature and scale. The important requirement is a simulation prediction that incorporates the above mechanisms and combinations of the mechanisms involving multiple wave components and interaction scales. For example, long time evolution involving multiple broadband resonant wave triads/quartets and direct and indirect forcing cannot be predicted based on individual mechanisms and/or narrow-band results. These effects must be obtained using large-scale direct wave simulation such as SNOW that includes modeling of all of the mechanisms.
These large-scale simulations can be used to obtain direct comparisons with proposed field measurements. Using direct simulation Monte-Carlo, we obtain also datasets that provide information on the statistical characteristics of surface wave dissipation as a function of mud layer variations and properties. These results are essential for the development of modeling of mud bottom dissipation effects for wave spectral prediction tools such as SWAN.
References
Alam, M.Z., Liu, Y. and D.K.P. Yue (2005). Efficient computation of nonlinear interactions of surface and internal gravity waves. Tech. Rept. Vortical Flow Research Laboratory, MIT.
Allouche, M., I.A. Frigaard and G. Sona (2000). Static wall layers in the displacement of two visco-plastic fluids in a plane channel. J. Fluid Mech., 424, 243-277.
Bercovier, M. and M. Engleman (1980). A finite element method for incompressible non-Newtonian flows. J. Comp. Phys., 36, 313-326.
Dade, W. B. (1992). Studies on boundary conditions for fine-sediment transport. Ph.D. Diss., Univ. Washington, Seattle, WA, 269pp.
Dalrymple, R.A. and P. L.-F. Liu (1978). Water waves over soft muds: a two-layer fluid model. J. Phys. Ocean.,8, 1121-1131.
Dalrymple, R.A. and P.L.-F. Liu (1982). Gravity waves over a poro-elastic seabed, Proc. Ocean Structural Dynamics Symposium, ASCE.
Dalrymple, R.A., J.T. Kirby and P.A. Hwang (1984). Wave diffraction due to areas of energy dissipation, J. Waterway, Port, Coastal ,Ocean Engrg. , ASCE, 110, WW1, 67-79.
Dean, R. G. and R. A. Dalrymple, (1991). Water Wave Mechanics for Engineers and Scientists. World Scientific, 368pp.
Dimas, A.A. and G.S. Triantafyllou (1994). Nonlinear-interaction of shear-flow with a free-surface. J. Fluid Mech., 260, 211-246.
Dommermuth, D.G. and D.K.P. Yue (1987). A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267-288.
Draut, A. E., Kineke, G. C., Huh, O. K., Grymes, J. M. III, Westphal, A., and C.C. Moeller, (2005) Coastal mudflat accretion under energetic conditions, Louisiana chenier-plain coast, USA., Mar. Geol., 214, 27-47.
Draut, A.E., Kineke, G.C., Velasco, D.W., Allison, M.A., and R.J. Prime (2005). Influence of the Atchafalaya River on Recent Evolution of the Chenier Plain Inner Continental Shelf, Northern Gulf of Mexico. Cont. Shelf Res., 25, 91-112.
Fairall, C. W., E. F. Bradley, J. E. Hare, A. A. Grachev, and J. B. Edson (2003). Bulk parameterization of air–sea fluxes: Updates and verification for the COARE algorithm. J. Climate 16, 571–591.
Flemming, B. W. (2002). Geographic distribution of muddy coasts, in Muddy Coasts of the World: Processes, Deposits and Functions, T. Healy, Y. Wang and J.-A. Healy. (eds) Amsterdam, The Netherlands, Elsevier Science B.V. p. 99-201.
Foda, M.A. (1989). Sideband damping of water waves over a soft bed. J. Fluid Mech., 201, 189-201.
Frigaard, I.A. and C. Nouar (2005). On the usage of viscosity regularization methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid Mech., 127, 1-26.
Gade, H.G. (1958) Effects of a nonrigid, impermeable bottom on plane surface waves, J. Marine Res., 16, 61-82.
Glowinski, R. (1983). Numerical Methods for Nonlinear Variational Problems. Springer-Verlag.
Haller, M.C., R.A. Dalrymple and I.A. Svendsen (2002). Experimental study of nearshore dynamics on a barred beach with rip channels, J. Geophys. Res., 107, C6.
Huang, X. and M.H. Garcia (1998). A Herschel-Bulkley model for mud flow down a slope. J. Fluid Mech., 374, 305-333.
Huerre, P. and P.A. Monkewitz (1990). Local and global instabilities in spatially developing flows. Ann. Rev. Fluid Mech., 22, 473-573.
Higgins, E. E. (2002). Effects of a muddy coast on wave attenuation: Gulf of Mexico, Louisiana. M.Sc. thesis, Dept. Geology & Geophysics. Chestnut Hill, MA, Boston College, 49pp
Hill, D. and Foda, M.A. (1998). Subharmonic resonance of oblique interfacial waves by a progressive surface wave. Proc. R. Soc. Lond. A, 454, 1129-1144.
Isobe, M. T.N. Huynh, and A. Watanabe (1992). A study on mud mass transport under waves based on an empirical rheology model. Proc. 23rd Intl. Conf. Coastal Engnrg., Venice, 3093-3106.
Janssen, P. (2004). The Interaction of Ocean Waves and Wind. Cambridge University Press, Cambridge, UK.
Jamali, M., G.A. Lawrence and B. Seymour (2003). A note on the resonant interaction between a surface wave and two interfacial waves. J. of Fluid Mech. 491, 1-9.
Jiang, L. and Z. Zhao (1989). Viscous damping of solitary waves over fluid-mud seabeds. J. Waterways, Ports, Coastal and Ocean Engrg., 115, 3, 345-362.
Jiang, Q. and A. Watanabe (1996). Analysis of mud mass transport under waves using an empirical rheological model, Proc. Intl. Conf. Coastal Engrg., 4174-4187.
Kemp, G. P. (1986). Mud deposition at the shoreface: wave and sediment dynamics on the chenier plain of Louisiana, Ph.D. diss., Louisiana State Univ., Baton Rouge LA, 149pp.
Kirby, R. (1988). High concentration suspension (fluid mud) layers in estuaries, in Physical Processes in Estuaries, J. Dronkers and W. van Leussen (eds). New York, Springer-Verlag, p.463-487.
Krone, R.B. (1963). A study of rheologic properties of estuarial sediments. Ser. Rep. 63-8, Hydraul. Eng. Lab. and Sanitary Res. Lab., Univ. of Calif., Berkeley.
Lee, S.C. and A.J. Mehta (1997). Problems in characterizing dynamics of mud shore profiles, J. Hydraulic Engrg., 123, 4, 351-361.
Liu, P.L.-F. and R.A. Dalrymple (1984). The damping of gravity water waves due to percolation, Coastal Engineering , 8, 33-49.
Liu, K.F. and C.C. Mei (1989). Slow spreading of a sheet of Bingham fluid on an inclined plane, J. Fluid Mech., 207, 505-529.
Liu, Y. and D.K.P. Yue (1998). On generalized Bragg scattering of surface waves by bottom ripples. J. of Fluid Mech. 356, 297-326.
Maa, P.Y. and A.J. Mehta (1988). Soft mud properties: Voigt model. J. Waterways, Port, Coastal and Ocean Engrg., 114, 765-770.
Maa, P.Y. and A.J. Mehta (1990). Soft mud response to water waves, J. Waterways, Port, Coastal and Ocean Engrg., 116, 634-650.
MacPherson, H. (1980). The attenuation of water waves over a non-rigid bed, J. Fluid Mech., 79, 721-742.
Mallard, W.W. and R.A. Dalrymple (1977). Water waves propagating over a deformable bottom, Proc. 9th Annual Offshore Tech. Conf., Paper 2895.
Mathew, J. (1992). Wave-mud interaction in mudbanks. Ph.D. dissertation, Cochin University of Science and Technology Cochin, Kerala, India, 132p.
Mehta, A. J. (2002). Mudshore dynamics and controls, in Muddy Coasts of the World: Processes, Deposits and Function, T. Healy, Y. Wang and J.-A. Healy (eds). Amsterdam, Elsevier Science B.V., pp 19-60.
Mei, C.C. (1989). The Applied Dynamics of Ocean Waves. World Scientific.
Mei, C.C. and K.-F. Liu (1987). A Bingham-Plastic model for a muddy seabed under long waves. J. Geophys. Res., 92, 14581-14594.
Mei, C.C., M. Stiassnie and D.K.P.Yue (2005). Theory and Applications of Ocean Surface Waves. World Scientific, 1136 pp.
Meneveau, C., Lund, T. S. & Cabot, W. H. (1996), A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech., 319, 353-385.
Pananastasiou, T.C. (1987), Flows of materials with yield. J. Rheol., 31, 385-404.
Pearson, J.R.A. (1976), Instability in non-Newtonian flow. Ann. Rev. Fluid Mech., 8, 163-181.
Rotondo, K. A. and S. J. Bentley (2003). Deposition and resuspension of fluid mud on the western Louisiana inner shelf. Trans. Gulf Coast Assoc. Geo. Societies, 53, 722-731.
Rotondo, K.A., and Bentley, S.J. (2004), Marine dispersal of fluvial sediments as fluid muds: old concept, new significance. In: E.D. Scott and A. H. Bouma, Depositional Processes and Reservoir Characteristics of Siltstones, Mudstones, and Shales, Soc. Sedimentary Geology Misc. Pub., p. 24-49.
Sakakiyama, T. and E.W. Bijker (1989). Mass transport velocity in mud layer due to progressive waves, J. Waterway, Port, Coastal and Ocean Engrg., 115,5, 614-633.
Shen, L. and D.K.P. Yue (2001). Large-eddy simulation of free-surface turbulence. J. Fluid Mech., 440, 75-116.
Shen, L., Zhang, X., Triantafyllou, M.S. and D.K.P. Yue (2003). Turbulent Flow over a Flexible Wall Undergoing a Streamwise Traveling Wave Motion. J. Fluid Mech., 484, 197-221.
Shen, L., Zhang, C. and D.K.P. Yue (2002). Free-surface turbulent wake behind towed ship models--experimental measurements, stability analyses and direct numerical simulations. J. Fluid Mech., 469, 89-120.
Shen, L., X. Zhang, D.K.P. Yue, and G.S. Triantafyllou (1999). The surface layer for free-surface turbulent flows. J. Fluid Mech., 386, 167-212.
Sheremet, A. and G. W. Stone (2003). Observations of nearshore wave dissipation over muddy sea beds. J. Geophys. Res., 108 (C11): 3357.
Sheremet, A., A. J. Mehta, B. Liu, and G. W. Stone, 2004. Wave-sediment interaction on a muddy inner shelf during Hurricane Claudette. Est. Coastal and Shelf Sci. 63, 225-233.
Shibayama, T., M. Okuno, and S. Sato (1990). Mud transport rate in mud layer due to wave action, Intl. Conf. Coastal Engnrg., ASCE, 3037-3049.
Shibayama, T. and N.N. An (1993). A visco-elastic-plastic model for wave-mud interaction, Coastal Engrg. in Japan, 36, 1, 67-89.
Sternberg, R. W., G. C. Kineke, and R. Johnson, (1991). An instrument system for profiling suspended sediment, fluid, and flow conditions in shallow marine environments. Cont. Shelf Res. 11, 109-122.
Sommerfield, C.K., C.A. Nittrouer and C.R. Alexander (1999). 7Be as a tracer of flood sedimentation on the northern California margin. Cont. Shelf Res., 19, 335-361.
Suh, K.D. and R.A. Dalrymple (1987). Offshore breakwaters in laboratory and the field, J. Waterway, Port, Coastal and Ocean Engrg., ASCE, 113, 2.
Traykovski, P., W.R. Geyer, J.D. Irish, and J.F. Lynch (2000). The role of density driven fluid mud flows for cross shelf transport on the Eel River continental shelf. Cont. Shelf Res. 20, 2113.
Triantafyllou, G.S. and A.A. Dimas (1989). Interaction of two-dimensional separated flows with a free surface at low Froude numbers. Phys. Fluids A., 1, 1813-1821.
Trowbridge, J. H. and G. C. Kineke (1994). Structure and dynamics of fluid muds on the Amazon continental shelf. J. Geophys. Res. 99, 865-874.
Tsai W. and D.K.P. Yue (1996). Computation of nonlinear free-surface flows. Ann. Rev. Fluid Mech. 28, 248-278.
Tsuruya, H. and Nakano, S. (1987). Interactive effects between surface waves and a muddy bottom, Proc. Coastal Sediments ’87, Kraus, N.C., ed., 50-62.
Wang, Y., T. Healy, SCOR Working Group 106 (2002). Definition, properties, and classification of muddy coasts, in Muddy Coasts of the World: Processes, Deposits and Function, T. Healy, Y. Wang and J.-A. Healy (eds). Amsterdam, Elsevier Science, 9-18.
Wells, J.T. (1978). Shallow-water waves and fluid-mud dynamics, coast of Surinam, South America, Tech. Rept. 257, Coastal Studies Institute, Louisiana State Univ., 56pp, April.
Wells, J. T. (1983). Dynamics of coastal fluid muds in low-, moderate, and high-tide-range environments. Canadian J. Fisheries and Aquatic Sci. 40(Suppl. 1): 130-142.
Wu, G. (2004) Direct simulation and deterministic prediction of large-scale nonlinear ocean wavefield, Ph.D Thesis, Massachusetts Institute of Technology, Cambridge, MA.
Wu, G., Liu, Y., and D.K.P. Yue (2005) Studying rogue waves using large-scale direct phase-resolved simulations, Proc. 14th 'Aha Huliko'a Winter Workshop, Rogue Waves, Honolulu, Hawaii.