Dynamic failure mechanisms in ceramics are fundamentally different than those in static failure. While static failure is dictated by a small number of large pre-existing defects, dynamic failure is governed by crack growth from a large number of multi-sized defects. Coalescence of this large number of cracks leads to finer fragmentation of the material, such that the material transforms into a granular medium. The Graham-Brady research group models the mechanisms of brittle dynamic failure in ceramics, including damage growth, fragmentation and granular flow of the fragmented material.
Abstracts from a few relevant publications |
|
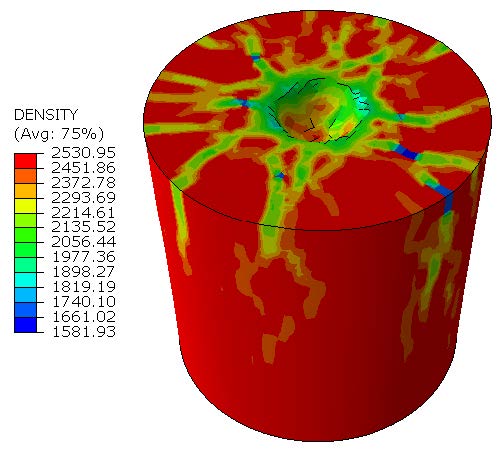
Failure modelling and sensitivity analysis of ceramics under impactA micromechanical multi-physics model for ceramics has been recalibrated and used to simulate impact exper-iments with boron carbide in ABAQUS. The dominant physical mechanisms in boron carbide have been identified and simulated in the framework of an integrated constitutive model that combines crack growth, amorphization and granular flow. The integrative model is able to accurately reproduce some of the key cracking patterns of Sphere Indentation experiments and Edge On Impact experiments. Based on this integrative model, linear regression has been used to study the sensitivity of sphere indentation model predictions to the input parameters. The sensitivities are connected to physical mechanisms, and trends in model outputs have been intuitively explored. These results help suggest material modifications that might improve material performance, prioritize calibration experiments for materials-by-design iterations, and identify model parameters that require more in-depth understanding. |
Bhattacharjee, A., Bhaduri, A., Hurley, R., Graham-Brady, L. (2021). “Failure modelling and sensitivity analysis of ceramics under impact,” ASME Journal of Applied Mechanics, accepted. |
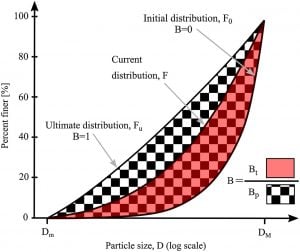
Constitutive Model for Brittle Granular Materials Considering Competition between Breakage and DilationA constitutive model is presented for brittle granular materials based on a recent reformulation of the breakage mechanics theory. The primary objective of the study is to capture peak strength with subsequent strain softening in dilatant specimens under shearing and the simultaneous evolution of breakage and dilation. The predictive performance of the model is assessed relative to two experimental datasets from the literature. The influence of the model parameters on the overall material response is described through a detailed calibration procedure based on a benchmark experimental dataset. Comparison of the results of drained triaxial compression experiments on two sands with the predictions of the model indicates that the enriched model can successfully capture the evolution of stress-strain behavior at different confinement levels. The predicted response of dilatant specimens exhibits stress- and density-dependent peak strength and strain softening toward the critical state, which is in agreement with experimental evidence. The simulations of Kurnell sand can reproduce the transition of the volumetric strain from <span id=”MathJax-Element-1-Frame” class=”MathJax” style=”font-style: normal; font-weight: normal; line-height: normal; font-size: 18px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px;” role=”presentation” data-mathml=”−0.05″>−0.05−0.05 to 0.14 as the confining pressure increases from 760 to 7,800 kPa. The predicted breakage of specimens subjected to different confining pressures is slightly higher than experimental measurements, whereas they exhibit similar trends. The proposed framework is capable of qualitatively reproducing many aspects of the experimentally observed stress-dilatancy-breakage relationship in brittle granular materials. |
Cil, M., Hurley, R., Graham-Brady, L. (2020). “Constitutive Model for Brittle Granular Materials Considering Competition between Breakage and Dilation,” Journal of Engineering Mechanics, 146(1): 04019110. |
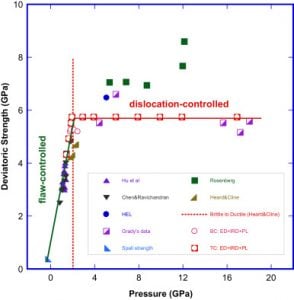
A 3D Mechanistic Constitutive Model for Brittle Materials Containing Evolving Flaw Distributions under Dynamic Multiaxial LoadingWe present a validated fully 3D mechanism-based micromechanical constitutive model for brittle solids under dynamic multiaxial loading conditions. Flaw statistics are explicitly incorporated through a defect density, and evolving flaw distributions in both orientation and size. Interactions among cracks are modeled by means of a crack-matrix-effective-medium approach. A tensorial damage parameter is defined based upon the crack length and orientation development under local effective stress fields. At low confining stresses, the wing-cracking mechanism dominates, leading to the degradation of the modulus and peak strength of the material, whereas at high enough confining stresses, the cracking mechanism is completely shut-down and dislocation mechanisms become dominant. The model handles general multiaxial stress states, accounts for evolving internal variables in the form of evolving flaw size and orientation distributions, includes evolving anisotropic damage and irreversible damage strains in a thermodynamically consistent fashion, incorporates rate-dependence through the micromechanics, and includes dynamic bulking based on independent experimental data. Simulation results are discussed and compared with experimental results on one specific structural ceramic, aluminum nitride. We demonstrate that this 3D constitutive model is capable of capturing the general constitutive response of structural ceramics. |
Hu, G., Liu, J., Graham-Brady, L. & Ramesh, K.T. (2015). “A 3D Mechanistic Constitutive Model for Brittle Materials Containing Evolving Flaw Distributions under Dynamic Multiaxial Loading,” Journal of the Mechanics and Physics of Solids, 78: 269-297. |
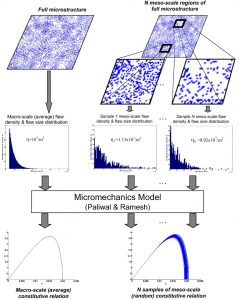
Statistical characterization of meso-scale uniaxial compressive strength in brittle materials with randomly occurring flawsIncreasingly fine spatial resolution in numerical models of brittle materials promises to improve prediction and characterization of dynamic failure in these materials. However, as the resolution of these numerical models begins to approach the material micro-scale, the associated discretization requires a definitive connection to the microstructure. In many cases a numerical model (e.g., a finite element mesh) that explicitly resolves each flaw within the material is not feasible for macro-scale analyses. As an alternative, each element can be treated as a meso-scale continuum with constitutive properties that reflect the characteristics of the underlying microstructure. Small scale elements will exhibit random variations in the constitutive properties as a result of the random variations in the number and types of flaws and the flaw sizes contained within each element. The present paper proposes a technique for assigning probability distributions to these element properties, which can be thought of as the meso-scale constitutive properties. In particular, the strain-rate dependent compressive uniaxial strength of a ceramic is modeled using a two-dimensional analytical model developed by Paliwal and Ramesh (2008). The effect on the probability distribution of meso-scale (or element-level) strength from flaw density, flaw size distribution, flaw clustering, and strain rate are studied. Higher strain rates, more flaw clustering, and decreasing element size all contribute to greater scatter in uniaxial compressive strength. Variations in flaw size increase the scatter in the strength more for low strain rate loadings and less clustered microstructures. The results provide interesting comparisons to the classical assumption of a two-parameter Weibull-distributed strength, showing that a three-parameter Weibull distribution and even a lognormal distribution fit better with the simulated strength data. |
Graham-Brady, L. (2010). “Statistical characterization of meso-scale uniaxial compressive strength in brittle materials with randomly occurring flaws,” International Journal of Solids and Structures, 47 (18-19): 2398-2413. |
Other relevant publicationsBhattacharjee, A., Hurley, R., Graham-Brady, L. (2022). “Fragmentation and granular transition of ceramics for high rate loading,” Journal of the American Ceramics Society, 105(5):3062-3080. *Selected for Best Paper Award Ramesh, K.T., Graham-Brady, L., Goddard, W.A., Hurley, R.C., Robbins, M., Tonge, A.L., Bhattacharjee, A., Clemmer, J.T., Zeng, Q., Li, W., Shen, Y., An, Q., Mitra, N. (2022). “Models for the behavior of boron carbide in extreme dynamic environments,” Journal of the American Ceramic Society, 105(5):3043-3061. Cil, M. B., Zeng, Q., Hurley, R. C., Graham-Brady, L. (2020). “An integrative model for the dynamic behavior of brittle materials based on microcracking and breakage mechanics,” Journal of the Dynamic Behavior of Materials, 6(4): 472-488. Huq, F., Liu, J., Tonge, A., Graham-Brady, L. (2019). “A micromechanics based model to predict micro-crack coalescence in brittle materials under dynamic compression,” Engineering Fracture Mechanics, 217: 106515. Cil, M., Hurley, R., Graham-Brady, L. (2019). “A rate-dependent constitutive model for brittle granular materials based on breakage mechanics,” Journal of the American Ceramics Society, 102(9): 5524-5534. Cereceda, D., Daphalapurkar, N., Graham-Brady, L. (2018). “One-dimensional models for dynamic fragmentation of brittle materials,” Dynamic Damage and Fragmentation, pp. 237-263, Wiley. Cereceda, D., Graham-Brady, L. & Daphalapurkar, N. (2017). “Modeling dynamic fragmentation of heterogeneous structural materials,” International Journal of Impact Engineering, 99:85-101. Liu, J. & Graham-Brady, L. (2016). “Perturbation-based surrogate models for dynamic failure of brittle materials in a multi-scale and probabilistic context,” International Journal for Multiscale Computational Engineering, 14(3): 273-290. Liu, J. & Graham-Brady, L. (2016). “Anisotropic Damage-Compliance Relationships for Brittle Materials under Compression,” International Journal of Solids & Structures, 100-101: 151-168. Katcoff, C.A. & Graham-Brady, L.L. (2014). “Modeling Dynamic Brittle Behavior of Materials with Circular Flaws or Pores,” International Journal of Solids & Structures, 51: 754-766. Daphalapurkar, N.P., Ramesh, K.T., Graham-Brady, L.L. & Molinari, J.F. (2011). “Predicting variability in the dynamic failure strength of brittle materials considering preexisting flaws,” Journal of the Mechanics & Physics of Solids, 59(2): 297-319. |
|