Machine Learning for Mechanics of Materials

Machine learning provides a host of incredibly powerful tools for efficient representations of material microstructure and mechanical behavior. Such representations enable probabilistic sampling and multi-scale modeling of materials at unprecedented structural scales; however, the uncertainty associated with these models remains an open research question. The Graham-Brady research group has looked at applications in simulation of two-phase and polycrystalline microstructures and in multi-scale modeling of composite materials, as well as uncertainty quantification of machine learning pipelines.

Abstracts from a few relevant publications

Probabilistic neural networks for uncertainty quantification in data-based materials modeling

Modern machine learning (ML) techniques, in conjunction with simulation-based methods, present remarkable potential for various scientific and engineering applications. Within the materials science field, these data-based methods can be used to build efficient structure–property linkages that can be further integrated within multi-scale simulations, or guide experiments in a materials discovery setting. However, a critical shortcoming of state-of-the-art ML techniques is their lack of reliable uncertainty/error estimates, which severely limits their use for materials or other engineering applications where data is often scarce and uncertainties are substantial. This paper presents methods for Bayesian learning of neural networks (NN) that allow consideration of both aleatoric uncertainties that account for the inherent stochasticity of the data-generating process, and epistemic uncertainties, which arise from consideration of limited amounts of data. In particular, algorithms based on approximate variational inference and (pseudo-)Bayesian model averaging achieve an appropriate trade-off between accuracy of the uncertainty estimates and accessible computational cost. The performance of these algorithms is first presented on simple 1D examples to illustrate their behavior in both extrapolation and interpolation settings. The approach is then applied for the prediction of homogenized and localized properties of a composite material. In this setting, data is generated from a finite element model, which permits a study of the behavior of the probabilistic learning algorithms under various amounts of aleatoric and epistemic uncertainties.

Olivier, A., Shields, M., Graham-Brady, L. (2021). “Probabilistic neural networks for uncertainty quantification in data-based materials modeling,” Computer Methods in Applied Mechanics and Engineering, 386:114079.

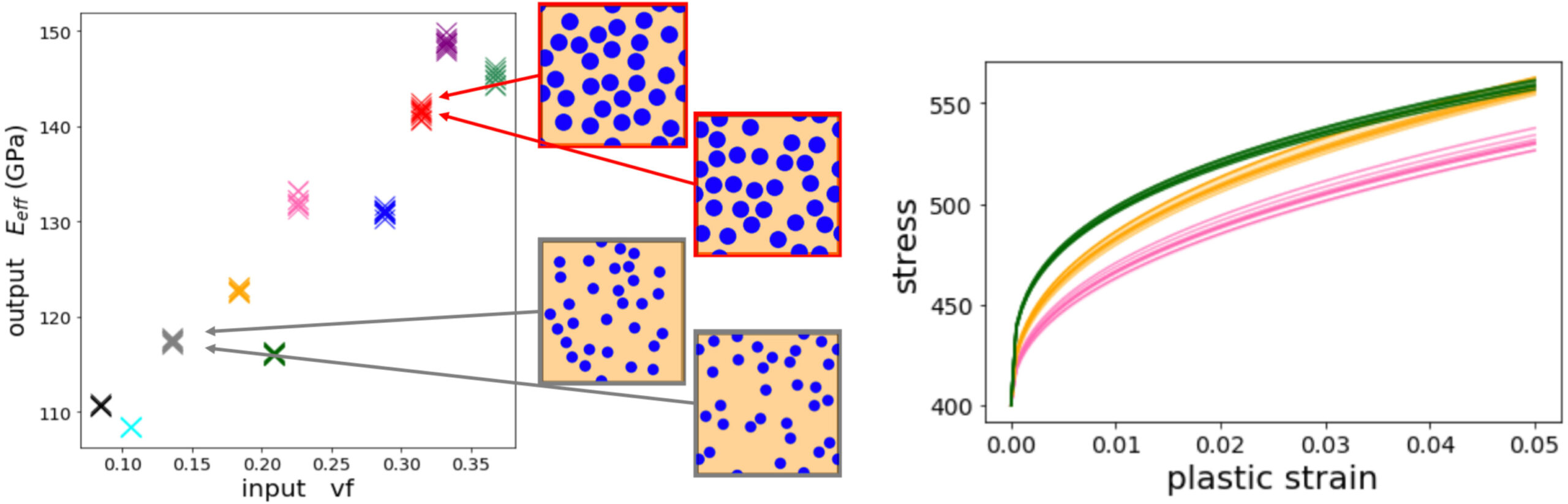
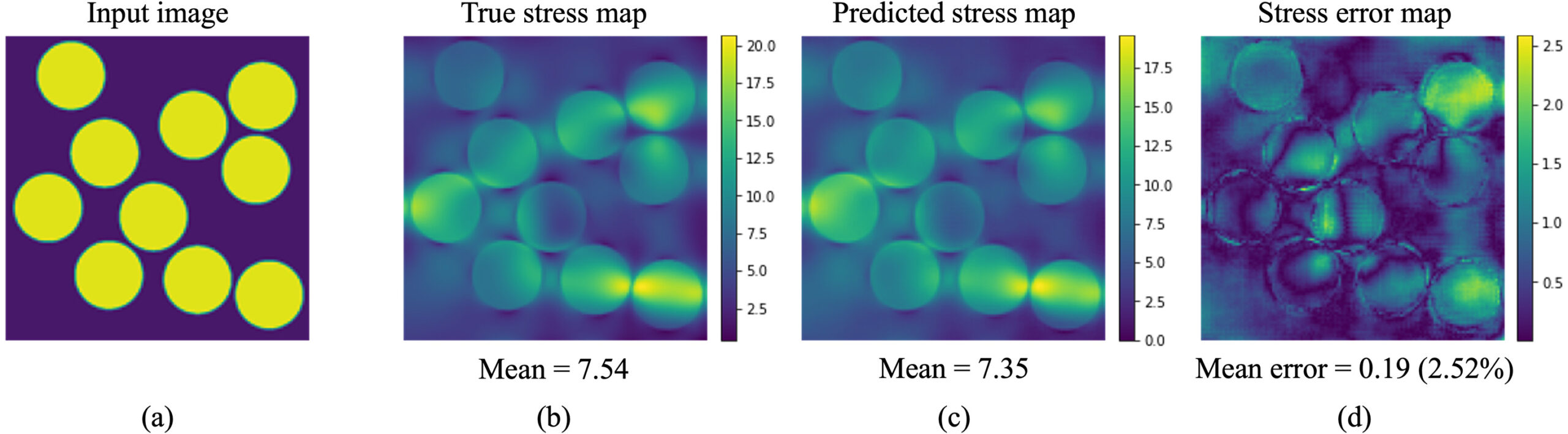
Stress field prediction in fiber-reinforced composite materials using a deep learning approach

Stress analysis is an important step in the design of material systems, and finite element methods (FEM) are a standard approach of performing computational analysis of stresses in complex material systems. The significant cost associated with multi-scale FEM analysis motivates replacement of FEM with a significantly faster data-driven machine learning based approach. In this study, we consider the application of deep learning tools to local stress field prediction in a fiber-reinforced matrix composite material system as an efficient alternative to FEM. The first challenge is to predict stress field maps for composite cross-sections with a fixed number of fibers and varying spatial configurations. Specifically, a mapping between the spatial arrangement of fibers and the corresponding von Mises stress field is achieved by using a convolutional neural network (CNN), specifically a U-Net architecture. The CNN is trained using data with the same number of fibers as the target systems. A robustness analysis uses different initializations of the training samples to find the evolution of the prediction accuracy with increasing number of training samples. Systems with a larger number of fibers typically require a finer finite element mesh discretization, leading to an increase in the computational cost. Thus, the secondary goal here is to predict the stress field for systems with larger number of fibers using CNNs that are pretrained on data from relatively cheaper systems with smaller fiber number.

Bhaduri, A., Gupta, A., Graham-Brady, L. (2022). “Stress field prediction in fiber-reinforced composite materials using a deep learning approach,” Composites Part B, 238: 109879.

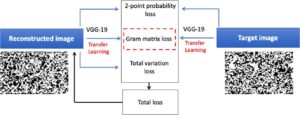
An efficient optimization based microstructure reconstruction approach with multiple loss functions

Stochastic microstructure reconstruction involves digital generation of microstructures that match key statistics and characteristics of a (set of) target microstructure(s). This process enables computational analyses on ensembles of microstructures without having to perform exhaustive and costly experimental characterizations. Statistical functions-based and deep learning-based methods are among the stochastic microstructure reconstruction approaches applicable to a wide range of material systems. In this paper, we integrate statistical descriptors as well as feature maps from a pre-trained deep neural network into an overall loss function for an optimization based reconstruction procedure. This helps us to achieve significant computational efficiency in reconstructing microstructures that retain the critically important physical properties of the target microstructure. A numerical example for the microstructure reconstruction of bi-phase random porous ceramic material demonstrates the efficiency of the proposed methodology. We further perform a detailed finite element analysis (FEA) of the reconstructed microstructures to calculate effective elastic modulus, effective thermal conductivity and effective hydraulic conductivity, in order to analyse the algorithm’s capacity to capture the variability of these material properties with respect to those of the target microstructure. This method provides an economic, efficient and easy-to-use approach for reconstructing random multiphase materials in 2D which has potential to be extended to 3D structures.

Bhaduri, A., Gupta, A., Olivier, A., Graham-Brady, L. (2021). “An efficient optimization based microstructure reconstruction approach with multiple loss functions,” Computational Materials Science, 199:110709.

Other relevant publications

Prameela, S.E., Pollock, T., Raabe, D., Meyers, M.A., Aitkaliyeva, A., Chintersingh, K.L., Cordero, Z., Graham-Brady, L. (2023). “Materials for Extreme Environments,” Nature Reviews Materials, 8(2): 81-88.

Maruyama, B., Hattrick-Simpers, J., Musinski, W., Graham-Brady, L., Li, K., Hollenbach, J., Singh, A., Taheri, M.L. (2022). “AI and Materials Research for Coupled Extremes,” MRS Bulletin, 47(11): 1154-1164.