Probabilistic Mechanics and Stochastic Finite Elements

All real materials exhibit random variations that affect structural reliability. Probabilistic mechanics tools such as stochastic finite elements provide a means of mapping probabilistic descriptors of materials to probabilistic descriptors of structural behavior. The Graham-Brady research group develops techniques for characterizing the uncertainty in material microstructure, in material properties and in identifying the variability of mechanics models.

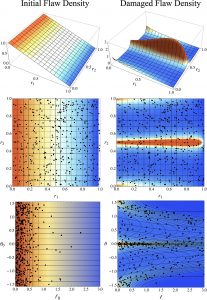
Abstracts from a few relevant publications

Three-dimensional microstructural information has become increasingly important to advanced computational modeling, and future developments in the field rely on continued maturation of the technology. In this work, a framework for analyzing the error associated with the collection of 3D datasets is proposed. The framework allows users to evaluate errors introduced into the data collection process through the selection of various experimental parameters. Synthetically generated microstructures, called phantoms, are used as a baseline. A simple model for microstructural data collection via electron backscatter diffraction is established. This model is used to simulate data collection from the phantom microstructures, in order to make observations about the effects of individual characterization parameter selection. By comparing simulations to the original phantoms, direct error measurements can be made. Results show how resolution, sample size, and noise can affect the quality of data sets. Finally, the framework is used to show how errors in computational models based on reconstructed microstructures are dependent on the choice of characterization parameters used to generate these microstructures.

Wade, N., Uchic, M., Criner, A., Graham-Brady, L. (2019). “A framework for quantifying effects of characterization error on the predicted local elastic response in polycrystalline materials,” Integrated Computational Materials Engineering (ICME) – Advancing Computational and Experimental Methods, Springer.

An Efficient Binning Scheme with Application to Statistical Crack Mechanics

A computational scheme is developed for sampling‐based evaluation of a function whose inputs are statistically variable. After a general abstract framework is developed, it is applied to initialize and evolve the size and orientation of cracks within a finite domain, such as a finite element or similar subdomain. The finite element is presumed to be too large to explicitly track each of the potentially thousands (or even millions) of individual cracks in the domain. Accordingly, a novel binning scheme is developed that maps the crack data to nodes on a reference grid in probability space. The scheme, which is clearly generalizable to applications involving arbitrary numbers of random variables, is illustrated in the scope of planar deformations of a brittle material containing straight cracks. Assuming two random variables describe each crack, the cracks are assigned uniformly random orientations and non‐uniformly random sizes. Their data are mapped to a computationally tractable number of nodes on a grid laid out in the unit square of probability space so that Gauss points on the grid may be used to define an equivalent subpopulation of the cracks. This significantly reduces the computational cost of evaluating ensemble effects of large evolving populations of random variables.

Huq, F., Brannon, R. & Graham-Brady, L. (2016). “An Efficient Binning Scheme with Application to Statistical Crack Mechanics,” International Journal for Numerical Methods in Engineering, 105(1): 33-62.

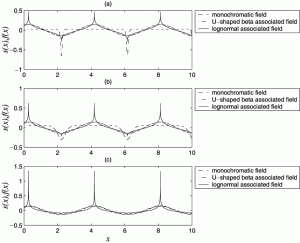
A hierarchy of upper bounds on the response of stochastic systems with large variation of their properties: random variable case

This paper is the first of a two-part series that constitutes an effort to establish spectral- and probability-distribution-free upper bounds on various probabilistic indicators of the response of stochastic systems. In this first paper, the concept of the variability response function (VRF) is discussed in some detail with respect to its strengths and its limitations. It is the first time that various limitations of the classical VRF are discussed. The concept of associated fields is then introduced as a potential tool for overcoming the limitations of the classical VRF. As a first step, the special case of material property variations modeled by a single random variable is examined. Specifically, beam structures with the elastic modulus being the only stochastic property are studied. Results yield a hierarchy of upper bounds on the mean, variance and exceedance values of the response displacement, obtained from zero-mean U-shaped beta-distributed random variables with prescribed standard deviation and lower limit. In the second paper that follows, the concept of the generalized variability response function is introduced and used with the aid of associated fields to extend the upper bounds established in this paper to more general problems involving stochastic fields.

Deodatis, G., Graham-Brady, L.L. & Micaletti, R. (2003). “A hierarchy of upper bounds on the response of stochastic systems with large variation of their properties: random variable case,” Probabilistic Engineering Mechanics, 18(4): 349-363.

Other relevant publications

Geyer, S., Papaioannou, I., Graham-Brady, L., Straub, D. (2022). “The spatial averaging method for non-homogeneous random fields with application to reliability analysis,” Engineering Structures, 253:113761.

Bhaduri, A., Brandyberry, D., Shields, M., Geubelle, P., Graham-Brady, L. (2020). “On the usefulness of gradient information in surrogate modeling: Application to uncertainty propagation in composite material models,” Probabilistic Engineering Mechanics, 60,103024.

Bhaduri, A., Gardner, J., Abrams, C., Graham-Brady, L. (2020). “Free energy calculation using space filled design and weighted reconstruction: A modified single sweep approach,” Molecular Simulations, 46(3):193-206.

Bhaduri, A., Meyer, C.S., Gillespie, J.W., Haque, B.Z., Shields, M.D., Graham-Brady, L. (2020). “A probabilistic modeling framework for composite plate penetration models under projectile impact,” under review.

Bhaduri, A. & Graham-Brady, L. (2018). “An efficient adaptive sparse grid collocation method through derivative estimation,” Probabilistic Engineering Mechanics, 51:11-22.

Bhaduri, A., He, Y., Shields, M., Graham-Brady, L., Kirby, R.M. (2018). “Stochastic collocation approach with adaptive mesh refinement for parametric uncertainty analysis,” Journal of Computational Physics, 371: 732-750.

Zeinoddini, V.M., Graham-Brady, L.L. & Schafer, B.W. (2013). “Imperfection sensitivity and reliability using simple bar-spring models for stability,” International Journal of Structural Stability and Dynamics, 13(3): Art.No. 1250075.

Tootkaboni, M. & Graham-Brady, L. (2010). “Stochastic direct integration schemes for dynamic systems subjected to random excitation,” Probabilistic Engineering Mechanics, 25(2): 163-171.

Tootkaboni, M., Graham-Brady, L. & Schafer, B. (2009). “Geometrically nonlinear behavior of structural systems with random material property: an asymptotic spectral stochastic approach,” Computer Methods in Applied Mechanics & Engineering, 198(37-40): 3173-3185.

Chung, D.B., Gutierrez, M.A., Graham-Brady, L.L. & Lingen, F.J. (2005). “Efficient numerical strategies for spectral stochastic finite element models,” International Journal of Numerical Methods in Engineering, 64: 1334-1349.

Deodatis, G., Graham-Brady, L.L. & Micaletti, R. (2003). “A hierarchy of upper bounds on the response of stochastic systems with large variation of their properties: random field case,” Probabilistic Engineering Mechanics, 18(4): 365-375.

Graham, L.L. & Deodatis, G. (2001). “Response and eigenvalue analysis of stochastic finite element systems with multiple correlated material and geometric properties,” Probabilistic Engineering Mechanics, 16(1): 11-29.

Graham, L.L. & Siragy, E.F. (2001). “Stochastic finite element analysis for elastic buckling of stiffened panels,” ASCE Journal of Engineering Mechanics, 127(1): 91-97.

Graham, L.L. (1998). “Maximum displacement variability of stochastic structures subject to deterministic earthquake loading,” Shock and Vibration, 5(5,6): 355-369.

Graham, L.L. & Deodatis, G. (1998). “Variability response functions for stochastic plate bending problems,” Structural Safety, 20(2): 167-188.