Simulation of Material Microstructure

Abstracts from a few relevant publications

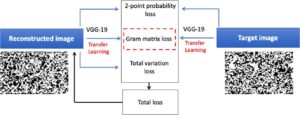
An efficient optimization based microstructure reconstruction approach with multiple loss functions

Stochastic microstructure reconstruction involves digital generation of microstructures that match key statistics and characteristics of a (set of) target microstructure(s). This process enables computational analyses on ensembles of microstructures without having to perform exhaustive and costly experimental characterizations. Statistical functions-based and deep learning-based methods are among the stochastic microstructure reconstruction approaches applicable to a wide range of material systems. In this paper, we integrate statistical descriptors as well as feature maps from a pre-trained deep neural network into an overall loss function for an optimization based reconstruction procedure. This helps us to achieve significant computational efficiency in reconstructing microstructures that retain the critically important physical properties of the target microstructure. A numerical example for the microstructure reconstruction of bi-phase random porous ceramic material demonstrates the efficiency of the proposed methodology. We further perform a detailed finite element analysis (FEA) of the reconstructed microstructures to calculate effective elastic modulus, effective thermal conductivity and effective hydraulic conductivity, in order to analyse the algorithm’s capacity to capture the variability of these material properties with respect to those of the target microstructure. This method provides an economic, efficient and easy-to-use approach for reconstructing random multiphase materials in 2D which has potential to be extended to 3D structures.

Bhaduri, A., Gupta, A., Olivier, A., Graham-Brady, L. (2021). “An efficient optimization based microstructure reconstruction approach with multiple loss functions,” Computational Materials Science, 199:110709.

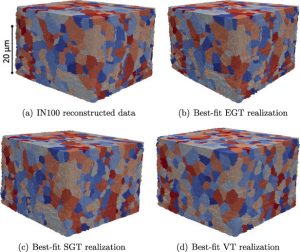
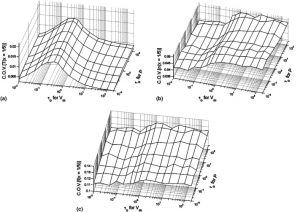
Grain growth tessellation models for polycrystalline microstructures

This work proposes novel models to represent and parametrize random morphology of polycrystalline microstructures. The reliability of high-fidelity mechanical analysis of polycrystalline microstructures depends upon the morphological representation of the virtual model. Two models addressed in this work are spherical growth and ellipsoidal growth tessellations in which grains grow as spheres (or ellipsoids) with random velocities which initiate from random nucleation sites represented by a spatial point process. All of the stochastic parameters can be represented by a marked point process random field model, for which simulation algorithms exist. Probability distributions of the model parameters are estimated by obtaining best-fit realizations of the models to a data set of a reconstructed microstructure specimen. The accuracy to which these tessellation models can represent real microstructures is evaluated using two example data sets by computing numerous microstructure features as well as the mismatch volume between the best-fit realizations and the data. The spherical growth and ellipsoidal growth tessellations demonstrate very significant improvements over the Voronoi tessellation, while remaining low dimensional representations of the microstructure. Realizations generated from a marked point process random field model show very good agreement in grain size, aspect ratio, and nearest neighbor distributions compared to an example data set. Thus, subsequent realistic instantiations of microstructures having the same statistical characteristics of the data can be trivially obtained, which are necessary to propagate the uncertainty associated with morphological randomness on response quantities of interest in mechanics-based applications.

Teferra, K. & Graham-Brady, L.L. (2015). “Grain growth tessellation models for polycrystalline microstructures,” Computational Materials Science, 102: 57-67.

Stochastic morphological modeling of random multiphase materials

A short-range-correlation (SRC) model is introduced in the framework of Markov/Gibbs random field theory to characterize and simulate random media. The Metropolis spin-flip algorithm is applied to build a robust simulator for multiphase random materials. Through development of the SRC model, several crucial conceptual ambiguities are clarified, and higher-order statistical simulation of random materials becomes computationally feasible. In the numerical examples, second- and third-order statistical simulations are demonstrated for biphase random materials, which shed light on the relationship between <span id=”MathJax-Element-1-Frame” class=”MathJax” style=”margin: 0px; padding: 0px; border: 0px; font-size: 16px; vertical-align: baseline; font-style: normal; font-weight: normal; line-height: normal; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px;” role=”presentation” data-mathml=”nth”>nthnth-order correlation functions and morphological features. Based on the observations, further conjectures are made concerning some fundamental morphological questions, particularly for future investigation of physical behavior of random media. It is expected that the SRC model can also be extended to third- and higher-order simulations of non-Gaussian stochastic processes such as wind pressure, ocean waves, and earthquake accelerations, which is an important research direction for high fidelity simulation of physical processes.

Graham-Brady, L. & Xu, X. Frank (2008). “Stochastic morphological modeling of random multiphase materials,” Journal of Applied Mechanics, ASME, 75(6): 0610011-06100110.

Stochastic simulation of non-Gaussian/non-stationary properties in a functionally graded plate

Composites with a graded profile between two distinct phases, titled functionally graded materials (FGM’s), have been proposed for a variety of applications. Many current numerical models of FGM’s overlook the inherent randomness observed in actual specimens, which arises due to the complexity and difficulty in tailoring the gradients to exact specifications during manufacturing processes. The effect of random variations, in both the component volume fractions and the porosity, on the response of a functionally graded metal/ceramic plate subjected to constant thermal boundary conditions is investigated in this work. These random variations are introduced into the FGM model via stochastic simulation. Of interest is the fact that the volume fraction and the porosity are both non-Gaussian and non-stationary. The non-stationarity is present due to the fact that the non-Gaussian probability density function describing both properties changes with location. Sample simulations are performed using a translation mapping from a stationary, standard Gaussian process to a non-stationary, non-Gaussian process. The results are used to quantify the effects of variations in the micromechanical configuration on the temperature, thermal stresses and safety factor within a functionally graded plate.

Ferrante, F.J. & Graham-Brady, L.L. (2005). “Stochastic simulation of non-Gaussian/non-stationary properties in a functionally graded plate,” Computer Methods in Applied Mechanics and Engineering, 194(12-16): 1675-1692.

Other relevant publications

Ferrante, F.J., Arwade, S.R. & Graham-Brady, L.L. (2005). “A translation model for non-stationary, non-Gaussian random processes,” Probabilistic Engineering Mechanics, 20(3): 215-228.