Stochastic Homogenization

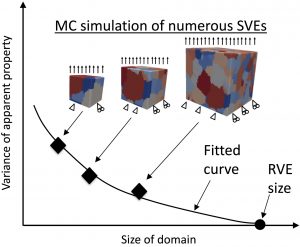
A random field-based method to estimate convergence of apparent properties in computational homogenization

This work addresses the challenge of efficiently determining the representative volume size in computational homogenization by exploiting the requirement that mechanical response quantities are statistically homogeneous and ergodic random fields. The proposed computational homogenization approach focuses on empirically determining the autocorrelation functions of output response quantities through post processing finite element analyses. Once the autocorrelation functions are known, only trivial computations are needed to determine the variance of apparent properties as a function of domain size without any additional finite element computation by utilizing a simple formula relating the autocorrelation function to the variance of spatially averaged quantities. This approach improves upon the current established approach by circumventing the need to analyze numerous successively larger domains in order to determine convergence of apparent properties, which can be computationally prohibitive. Furthermore, similar previous analytical expressions for the variance of apparent properties are asymptotic with respect to domain size while the expression in the proposed approach is exact. After presenting the formulation, the method is first demonstrated for a one-dimensional bar model where analytical expressions can be derived. Then the approach is demonstrated on two numerical examples: (1) a plane strain, linear elastic domain with a lognormal random field describing its compliance, and (2) a stochastic polycrystalline microstructure of a Nickel super alloy having a crystal plasticity model for its constitutive law.

Teferra, K. & Graham-Brady, L. (2018). “A random field-based method to estimate convergence of apparent properties in computational homogenization,” Computer Methods in Applied Mechanics and Engineering, 330: 253-270.

A Multi-scale Spectral Stochastic Method for Homogenization of Multi-Phase Periodic Composites with Random Material Properties

In this work a spectral stochastic computational scheme is proposed that links the global properties of multi‐phase periodic composites to the geometry and random material properties of their microstructural components. To propagate the uncertainties associated with the material properties to the microstructural response the scheme benefits from a combination of homogenization theory built into a finite element framework and the spectral representation of uncertainty based on Hermite Chaos where a probabilistic characterization of the solutions to a set of local problems defined on the period cell is first sought. A full stochastic description of the global (effective) properties is then obtained by averaging the solutions to the forgoing set of local problems over the unit cell. A representative subset of results is compared with the results obtained using Monte Carlo simulation to demonstrate the accuracy of the proposed procedure.

Tootkaboni, M. & Graham-Brady, L. (2010). “A Multi-scale Spectral Stochastic Method for Homogenization of Multi-Phase Periodic Composites with Random Material Properties,” International Journal of Numerical Methods in Engineering, 83(1): 59-90.

Simulation of local material properties based on moving-window GMC

When analyzing the behavior of composite materials under various loading conditions, the assumption is generally made that the behavior due to randomness in the material can be represented by a homogenized, or effective, set of material properties. This assumption may be valid when considering displacement, average strain, or even average stress of structures much larger than the inclusion size. The approach is less valid, however, when considering either behavior of structures of size at the scale of the inclusions or local stress of structures in general. In this paper, Monte Carlo simulation is used to assess the effects of microstructural randomness on the local stress response of composite materials. In order to achieve these stochastic simulations, the mean, variance and spectral density functions describing the randomly varying elastic properties are required as input. These are obtained here by using a technique known as moving-window generalized method of cells (moving-window GMC). This method characterizes a digitized composite material microstructure by developing fields of local effective material properties. Once these fields are generated, it is straightforward to obtain estimates of the associated probabilistic parameters required for simulation. Based on the simulated property fields, a series of local stress fields, associated with the random material sample under uniaxial tension, is calculated using finite element analysis. An estimation of the variability in the local stress response for the given random composite is obtained from consideration of these simulations.

Graham, L.L. & Baxter, S.C. (2001). “Simulation of local material properties based on moving-window GMC,” Probabilistic Engineering Mechanics, 16(4): 295-306.

Other relevant publications

Yaghoobi, M., Stopka, K.S., McDowell, D.L., Graham-Brady, L., Teferra, K. (2023). “Effect of sample size on the maximum value distribution of fatigue driving forces in metals and alloys,” submitted.

Teferra, K. & Graham-Brady L. (2019). “The maximum value distribution of response quantities in computational homogenization,” Journal of Engineering Mechanics, 145(5): 06019002.

Acton, K. & Graham-Brady, L. (2010). “Elasto-plastic mesoscale homogenization of composite materials,” Journal of Engineering Mechanics, ASCE, 136(5): 613-624.

Acton, K. & Graham-Brady, L. (2009). “Mesoscale modeling of plasticity in composites,” Computer Methods in Applied Mechanics & Engineering, 198(9-12): 920-932.

Tregger, N., Corr, D., Graham-Brady, L. & Shah, S. (2007). “Modeling mesoscale uncertainty for concrete in tension,” Computers & Concrete, 4: 347-362.

Tregger, N., Corr, D., Graham-Brady, L. & Shah, S. (2006). “Modeling the effect of mesoscale randomness on concrete fracture,” Probabilistic Engineering Mechanics, 21(3): 217-225.

Xu, X.F. & Graham-Brady, L. (2006). “Computational stochastic homogenization of random media elliptic problems using the Fourier Galerkin method,” Finite Elements in Analysis and Design, 42(7): 613-622.

Xu, X.F. & Graham-Brady, L.L. (2005). “A stochastic computational method for evaluation of global and local behavior of random media,” Computer Methods in Applied Mechanics & Engineering, 194(42-44): 4362-4385.

Baxter, S.C., Graham-Brady, L.L. & Xu, X.F. (2005). “Modeling the effects of material nonlinearity using moving window micromechanics,” International Journal for Nonlinear Mechanics, 40: 351-359.

Graham, L.L., Gurley, K. & Masters, F. (2003). “Non-Gaussian simulation of local material properties based on a moving-window technique,” Probabilistic Engineering Mechanics, 18(3): 223-234.

Graham-Brady, L.L., Siragy, E.F. & Baxter, S.C. (2003). “Analysis of heterogeneous composite materials using moving-window techniques,” Journal of Engineering Mechanics, ASCE, 129(9): 1054-1064.

Corr, D.J. & Graham, L.L. (2002). “Mechanical analysis of concrete with the moving-window generalized method of cells,” ACI Materials Journal, 100(2): 156-164.

Baxter, S.C., Hossain, M.I. & Graham, L.L. (2001). “Micromechanics based random material property fields for particulate reinforced composites,” International Journal of Solids & Structures, 30: 9209-9220.

Baxter, S.C. & Graham, L.L. (2000). “Characterization of random composite materials using the moving-window generalized method of cells technique,” ASCE Journal of Engineering Mechanics, 126(4): 389-397.