Internal Forces
The only internal force that will be investigated is axial tension in the cables, since that is the only force that the cables are able to resist. The reaction forces found at the tower and anchor are the values of the internal axial force components in the cables at the points of support and will be used to find the axial forces.
Referring to the discussion of
force components from the analysis of the
The total axial force will also decrease with the slope, but not linearly.
The axial force can be found by using trigonometric relationships of the two perpendicular components. First the angle at the point in question is found from
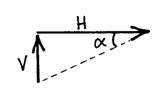
as already used to find the cable angles at the supports. This angle is used with the values of the vertical and horizontal components to find the resulting axial force, N, in the formula:
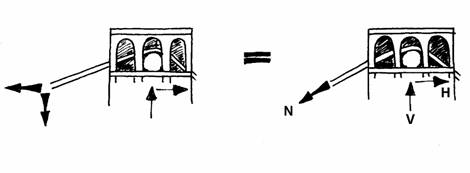
To illustrate this, the axial force in the cables will be found at a number of different points, first at the supports where the angles are known.
On the main span side of the
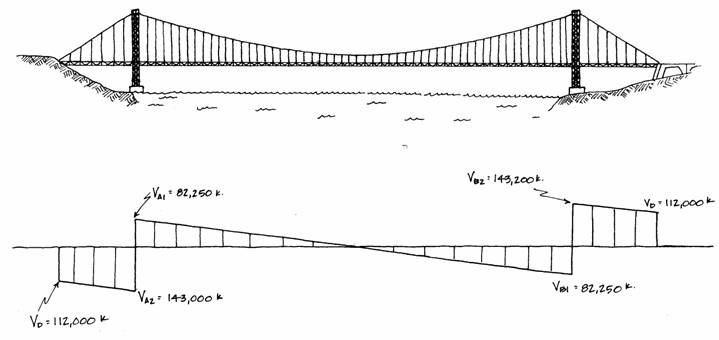
towers, the cables are inclined at an angle of . They have a vertical component of 82,250 kips
and a horizontal component of 220,000 kips.
Then the axial tension force, N, is:
On the other side of the tower
support, the cables have a slope of where they meet the towers. The vertical reaction is 143,000 kips, and as
always, the horizontal reaction is 220,000 kips. The axial force is found from these values as
This value is about 10% larger than the value on the other side of the tower support. The horizontal component is the same, so the increase is caused by the vertical component which is larger because of the slope of the cables.
At the anchor the axial force can be found from the corresponding angle, vertical and horizontal components as:
At the midpoint of the main span the slope of the cable is zero, i.e., at the point where it changes from curving downward to curving upward.
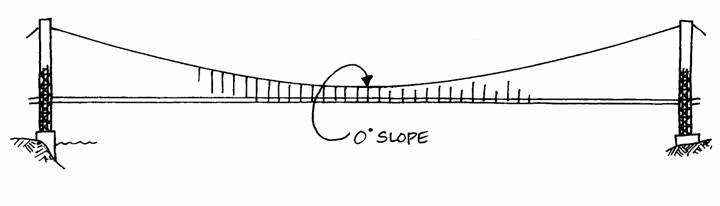
The internal tensile force is
found using only the known angle of and the horizontal component (220,000 kips) because
the vertical component is zero.
Because there is no slope at this point, the tensile force reaches its minimum here. As the angle increases elsewhere in the cables, so does the value of the internal axial tension force.
To find the value at any other point along the cables, one must know the slope of the cable and the value of the vertical component at that point. The angle can be found from formulas that describe the shape of the cable. The vertical force component is found from the diagram shown earlier. From structural principles that will be developed in the next analysis, the cables are known to take the shape of a parabola. This is the only form that a flexible structure under uniform load can have. A flexible structure has the natural inclination to this shape so that all its internal forces are axial and tensile. This is most easily understood by imagining a string under any loading:
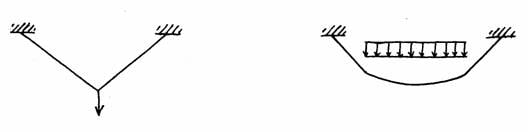
This principle is similar to that
mentioned in the a structure that follows the diagram of its
bending moments will use its material most efficiently to resist them. The bending moments that would act on a cable
if it could resist them describe a parabola; therefore, a cable must take this
parabolic shape to act in tension. (This
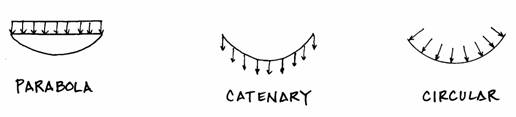
idea will be further investigated in the next analysis.) The parabolic shape results from a uniform
load on a flexible structure; in this case it is mainly the road deck. If the cables were to act under their weight alone,
they would hang in a shape similar to a parabola, but slightly different
a catenary.
This shape is different because the cables own weight would not be
uniform in its deflected position. Both
these shapes can be contrasted to a circle which is created by a uniform
pressure, like air in a balloon.
Since the cables are parabolic,
their quarterpoints will have an angle of found from the formula for the quarterpoints
of a parabola:
where d is the depth of the parabola at the midpoint, 327 feet, and l is 3500 feet. The vertical force component will have a value halfway between 82,250 kips and zero: 41,125 kips. Therefore, the axial force at the quarter points of the main span is:
The axial forces have been shown to vary along the span of the cables. The values found are called out on the following diagram for comparison.
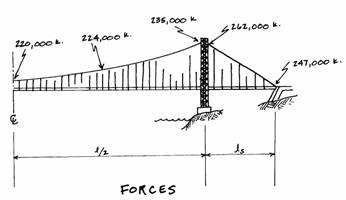
One can see that the forces in the side span cables are greater, but since the four spanning cables are continuous, they all have the same area over their entire lengths. (These forces area total of those in each cable, i.e., the force in each cable is one-fourth of those shown.)
Introduction Geometry Loads Reactions Internal Forces Stresses Efficiency Explore