Reactions

 

Introductory Principles          Main Span Reactions          Side Span Reactions

 

 

The loads on the bridge will be transferred through the cables to the tower supports and finally to the anchor supports.  This analysis will not investigate the reactions at the bases of the towers because the cables are the topic here.  Therefore, we will study the reactions at the ends of the cables (in the anchors) and at the tops of the tower.  Because of the idealization of symmetry, the reactions only need to be found at one tower and one anchor.

 

 

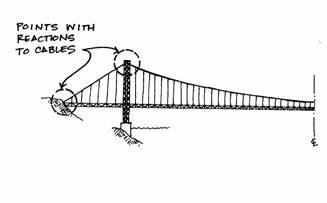
Because of their flexibility, cables can change their shape so that any applied load will only create tensile forces in them.  Thus the cables develop the graceful curvature that is so characteristic of suspension bridges.  The curvature inclines the cables at the point where they are supported.  The tensile force that is acting along the axis of a cable must be resisted by both a horizontal and a vertical reaction.

 

 

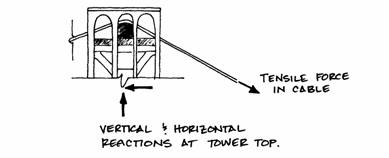
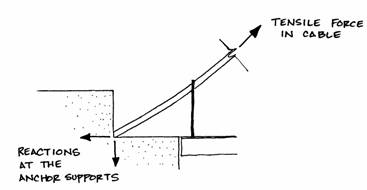
This is the same at the anchor where the cables come in at an angle.

 

 

The reaction forces can be found by taking advantage of the cables’ inability to resist bending moment at any point, i.e., the bending moment will be zero all along the cable.  Since the bending moment is zero, one can find the force that would create moments around any point of the cable and set the sum of them equal to zero.  For example, the bending moment at the hinge shown is zero, and, therefore, if the member is to be in equilibrium (immobile) the bending moments acting on it must balance.  If the bending moment of each force is found, one will see that they cancel because they are trying to turn the member in opposite directions.

 

 

 

 

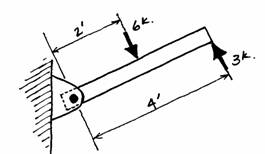
The sum of the moments about a hinge is zero (  ). This can be seen in the equation:

 

 

 

 

Main Span Reactions

 

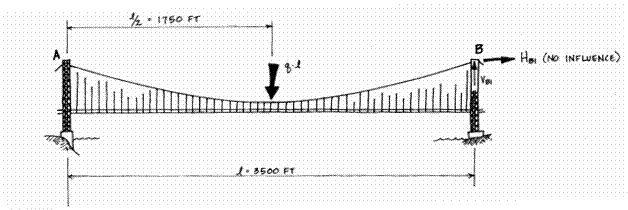
This same principle can be applied to the cables.  Concentrating first on the main span, the reactions in the tower supports can be found.  If the endpoint of the main span (A) is picked for convenience, the forces acting on the cables will balance around it because .

 

 

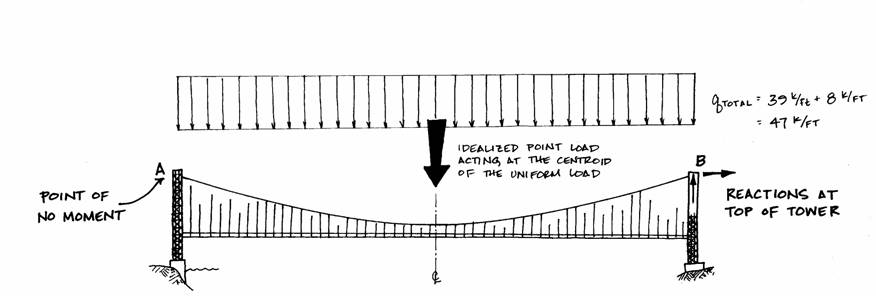
The horizontal reaction at point B creates no bending moment around point A.  This is because it is acting along the imaginary line that would connect points A and B.  The vertical reaction, however, would create a bending moment around point A. The magnitude of this bending moment is equal to the distance multiplied by the force:

 

 

 

The other force created by a bending moment around point A is the load on the cables  both dead and live loads.  This uniform load will be idealized by a point load which will act at the midpoint of the span.  The magnitude of this point load is:

 

 

 

This force will act a distance of  from point A.

           

 

 

 

 

 

From  the magnitude of the vertical reaction can be found by:

 

 

 

                   -                   

 

 

 

The total load and vertical reaction act in opposite directions, so one must be considered negative.  Substituting in the known values of  and  and rearranging the equation, one finds:

 

 

 

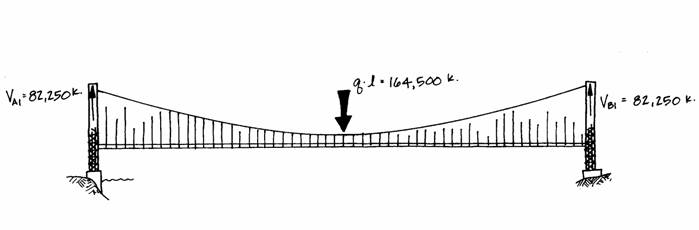
The vertical reaction at the left-hand tower is found through a vertical force balance, i.e., the forces acting upward (reactions) must equal the forces acting downwards (the loads).

 

 

 

This result shows that the vertical reactions at the ends of a symmetrical span are equal.

 

 

Now that the vertical reactions are known, the horizontal reactions from the main span can be found.  The same principle of a moment balance can be applied to find the horizontal reactions, this time finding the moments about the centerpoint of the cable, .  Working with one side of the cables, one finds the following set up of forces.

 

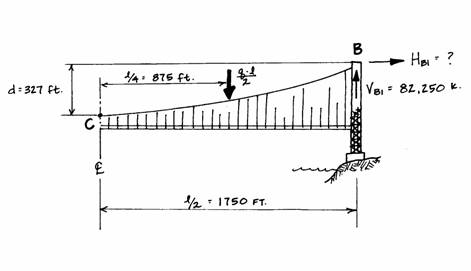
The load, , is found as 82,250 k and acts at a distance  from point C.  The bending moments around the center can be set equal to zero and then the horizontal reactions can be found:

 

 

 

           -                                               -                  

 

where:   

Rearranging, we can solve for :

           

 

 

           

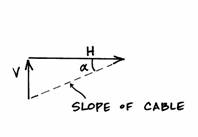
The values of the horizontal and vertical reactions can be used to find the slope of the cables where they meet the supporting tower.  (This angle will be necessary in subsequent calculations of internal force). 

 

 

 

 

 

 

 

Side Span Reactions

 

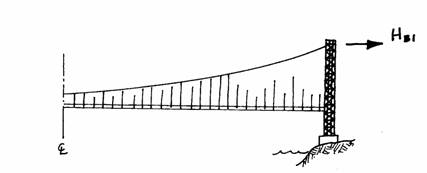
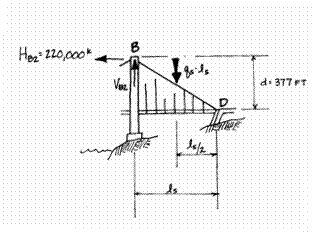
The reactions in the side spans will be investigated next.  The value of the load on the spans is found from  and .  The horizontal reaction at the tower is known because the analysis has assumed that no horizontal force will be exerted on the tower; therefore, the horizontal reaction to the loads on the side span is equal and opposite to the horizontal reaction already found.

 

 

 

 

 

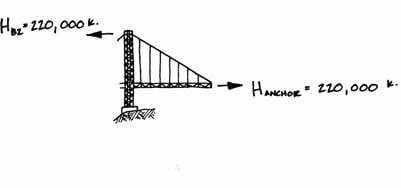
To find the remaining reactions in the side spans, that portion of the bridge will be isolated and the horizontal reaction retained as a force.  To create a horizontal equilibrium, i.e., have all the horizontal forces balance, the horizontal reaction in the anchor must have this same value H = 220,000 k. 

 

The vertical reaction at the tower can be found by applying the moment balance principle around the anchor point, D.  Forces that will create moment are both the vertical and horizontal reactions at the top of the tower and the loads suspended from the cables.  The vertical reaction is the unknown force that will be found from this balance.  The load from  and  is found over the side span length of 650 feet:

 

 

 

This force acts a distance of  from point D. 

 

 

 

 

                             +              -             

 

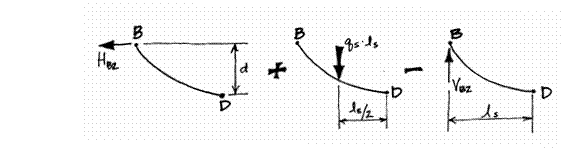
Therefore:

 

 

 

 

This value is added to the value of V_B1 which is the vertical reaction developed by the load on the main span.  Together the values show the total vertical reaction at the top of the tower.

 

 

 

To find the vertical reaction at the anchor, the principle of vertical equilibrium is used  all the vertical forces on the side spans must balance.

 

 

 

 

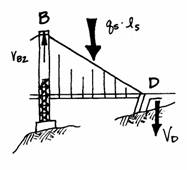
This reaction is unlike any vertical reaction encountered thus far in the analysis.  Usually a vertical reaction is reacting against compressive forces  forces that would push the structure into the ground.  At the anchor, however, the forces are tensile and are trying to pull the cable out of the anchor block of concrete.

 

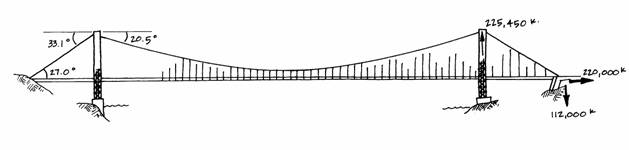
The side spans meet the tower at an angle of  and the anchor at an angle of  as found from the following calculations:

 

 

 

This analysis has idealized the bridge as symmetrical, so the tower and anchor reactions, as well as the angles on the left-hand side will be equal and opposite to those found on the right-hand side.  Now all the reactions, both horizontal and vertical, have been found in all four supports of the bridge.

 

 

 

 

 

 

Introduction     Geometry     Loads     Reactions     Internal Forces     Stresses     Efficiency     Explore

 

Structural Studies Home